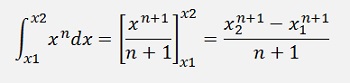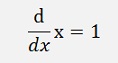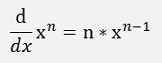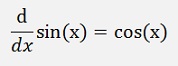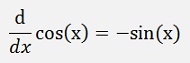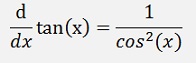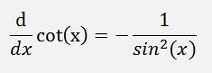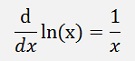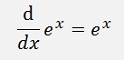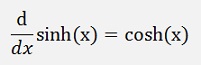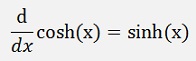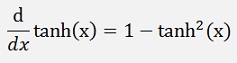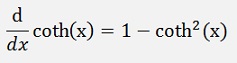Differentiation
Product rule
Chain rule
Quotient rule
Logarithmic differentiation
Integration
Some basic differentiation formulas
Differentiation
In physical science sometimes it is necessary to know the rate of the change of a given value. A simple sample is the speed of a car which is the rate of the change of the position of this car. Graphically that means if the draw the trend of the value in a graphic we lay a tangent onto this graphic:

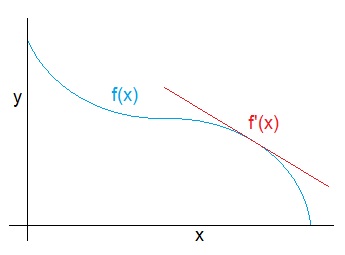
If the graphic is a function of the value x called f(x) = y, the rate of change is the differentiation f’(x). This can as well be written as
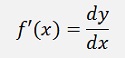
For the derivation of f’(x) we have to start with the situation of a small change of x and look how this affects y:
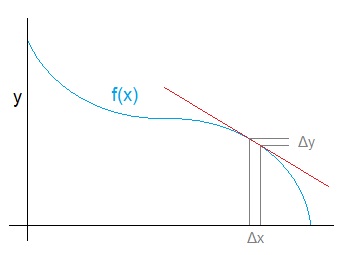
A small change of x as a Δx results in a small change of y as Δy. If we divide Δy by Δx we get a approximated rate of change for y. That is already close to the differentiation f’(x). The smaller Δx is the closer we get f’(x). If Δx would be infinitesimal, Δy divided by Δx would be exactly the differentiation f’(x) at the point x. If f’(x) should be calculated out of f(x), this is the procedure. Build the equation for Δy divided by Δx and let Δx become infinitesimal. That sounds easy. But that’s not always case. If we for instance want to calculate the differentiation of the function x2, that would be like:
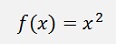
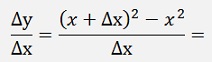
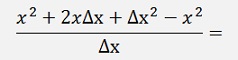
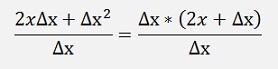
and so
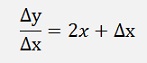
If Δx is infinitesimal
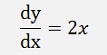
That’s basically the idea. We have to get an equation for Δy / Δx where Δx is in a form that does not influence the rest of the term on the right side and the Δx part just vanishes if it becomes infinitesimal.
The above sample can be extended to:
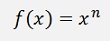
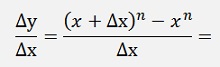
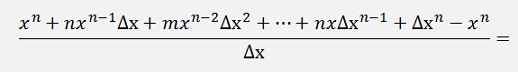
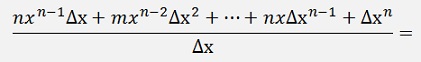
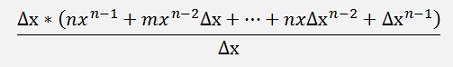
We don’t have to consider all the coefficients of (x + Δx)^n as every one that contains a Δx will vanish anyway (the factor m is a binominal coefficient and its value is not too important for the moment).
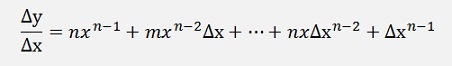
If Δx is infinitesimal
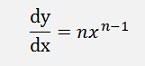
Another interesting sample is the differentiation of the trigonometric function sin(x):
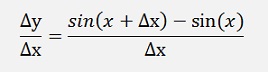
as
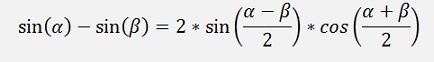
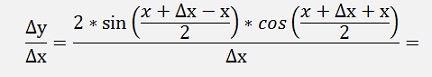
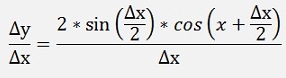
The sinus function can be written as a Taylor polynomial (See Taylor polynomials):
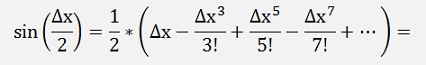
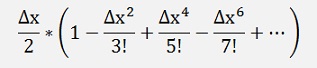
and so
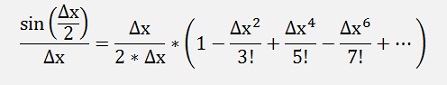
and that becomes 1/2 if Δx becomes infinitesimal.
That means
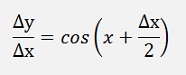
and
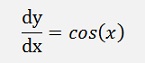
The same procedure again. Bring the formulation into a form where the Δx part on the right side vanishes if Δx becomes infinitesimal. That’s the basic approach

Now there are situations where that does not work and the function to be differentiated must be dissected in parts that can be differentiated one by one and the differentiation of the origin function is the sum of the differentiations of these parts like:
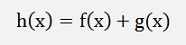
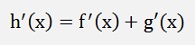
There are some rules for this:
If the function to be differentiated is the product of 2 functions, the product rule has to be used:
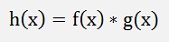
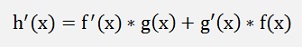
According to the dissection of Weierstrass from the point f(a) the value f(x) can be approximated by:
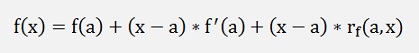
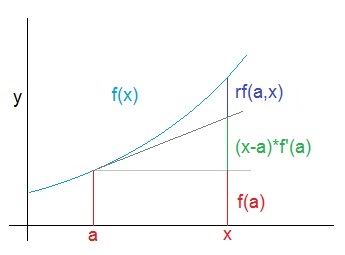
with rf(a,x) = 0 if x – a becomes 0.
With this we write
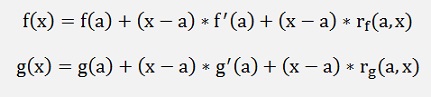
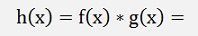
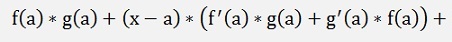
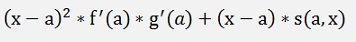
with
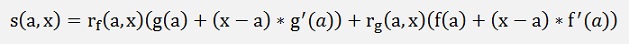
If x – a becomes 0 => s(a,x) = 0 and
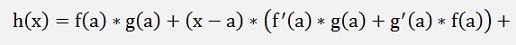
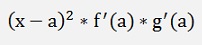
with h(a) = f(a)*g(a)
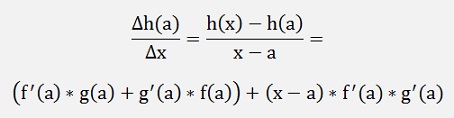
And if x – a becomes 0
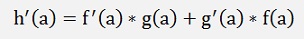
If the function to be differentiated is a chain of 2 functions:
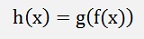
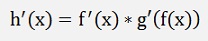
One more time Weierstrass :
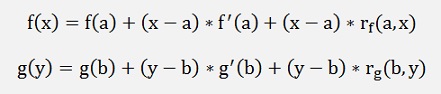
with y = f(x) and b = f(a)
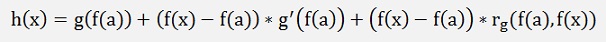
If x – a becomes 0 => rg(f(x),f(a)) = 0 and
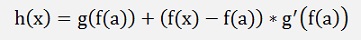
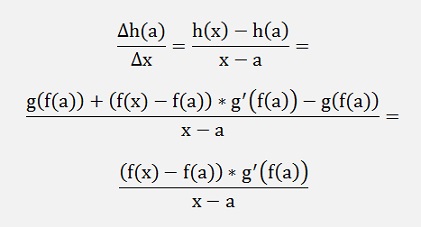
If x – a becomes 0
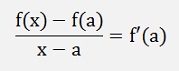
and
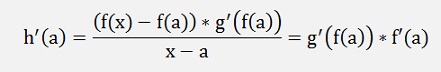
1)
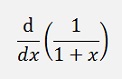
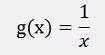
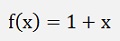
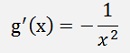
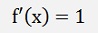
and with this:
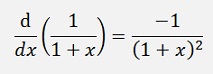
2)
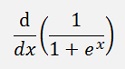
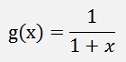
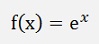
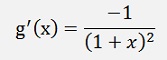
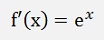
and with this:
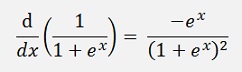
3) The Sigmoid function
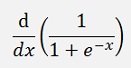
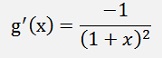
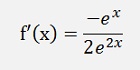
and with this:
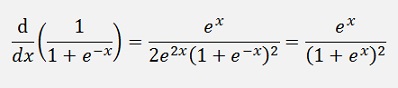
If the function is the quotient of 2 functions:
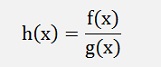
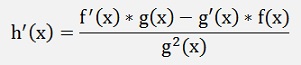
The proof is done the same again:

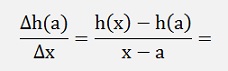
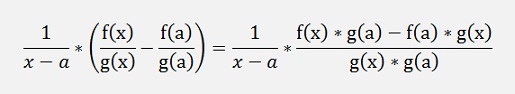
If we replace f(x) and g(x) by the formulas from above:
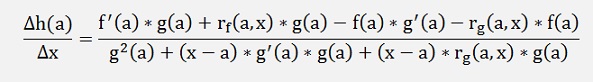
If x – a becomes 0 =>
rf(a,x) =0 and rg(a,x) =0
and we get
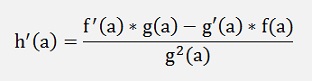
Logarithmic differentiation
A function like
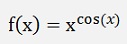
is not directly derivable.
To differentiate such a function, the logarithm of both sides of the equation can be built like:
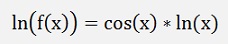
This equation can be differentiated on both sides now.
On the left, side with the chain rule, we get
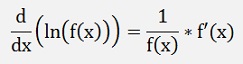
On the right side, using the product rule:
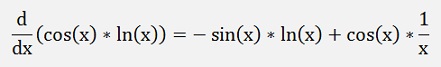
Both inserted in the above equation
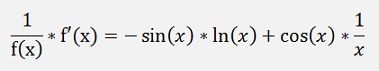
This can be resolved for f’(x)
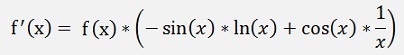
Or with the origin formulation
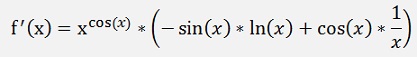
Quite a handy approach

Integration is the reversal of differentiation. If we have a car moving at a certain speed again, the distance it makes is the integration of its speed over the time.For the derivation of this we have a look at this speed what is the differentiation f’(x) of the position f(x). With x as time and y as the position:
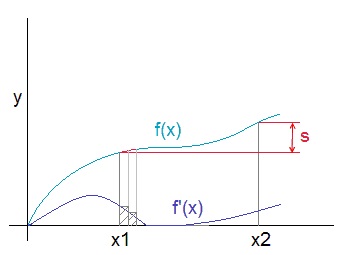
To calculate the distance the car made within the time x2-x1 we define e small time span Δx. If we multiply this time span by the speed at x1, we get the distance the car made between x1 and x1+ Δx in a good approximation. Now we multiply the speed at x1+ Δx by Δx and get the distance made between x1+ Δx and x1+ 2*Δx. If we do this for the entire time x1 till x2 and take the sum of all these small pieces, we get a good approximation of the distance the car made and if Δx becomes infinitesimal, the calculation will be exact and the calculation is the integration of f’(x) from x1 till x2. The point now is the fact that the distance we calculated is nothing else than f(x2) – f(x1). That means if we want to integrate a function f’(x) from x1 till x2 its f(x2) – f(x1). So if we want to integrate a random function f(x), we have to find the function g(x) whose differentiation g’(x) = f(x). What is the reversal of the integration.
For instance if we want to integrate the function xn.