Mosi's Math

Vector calculations

During studies I regarded vector calculations as a terrible discipline. I remember quite well: At the end of the first week of school a teacher “performed” the calculation of the balance point of a triangle by the use of vectors. At the end of this performance one of the students packed his staff, said that was it for me, quit the school and never came back. It was really awful...I tell you :-)

Now everything is different. I learned to like vectors and use then quite often. If something has to be calculated in the 3 dimensional spaces, it has to be done by the usage of vectors. No big deal.

By the way: 2 dimensional vectors should not be mixed up with complex numbers as these are really different things. I think that’s an important point.

Definition of a vector

A vector is pure mathematically expressed a directed route in multi-dimensional spaces, whereas multi means more than 1 dimension. A vector has a direction and a length. Usually it is defined by its expansion in each coordinate axis like (for instance in 3 dimensional space)

It is basically a matrix with just 1 column and can mathematically be treated like that.

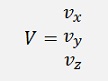
To identify a vector is done in different ways. Some put an arrow on top of the sign some don’t. Some write the sign of a vector in strange gothic characters and some just write a capital letter for a vector similar to the sign for a matrix. So do I.

The length of a vector in 3 dimansional spaces is according to Pythagoras:

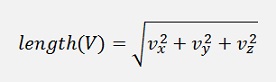
or in multi-dimensional spaces:

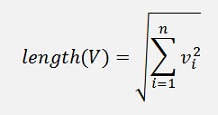
the root of the sum of the square of all expansions. This length is quite often named the norm of the vector and it’s sign is

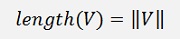
There are different kinds of norms defined:

-The Maximum norm is the maximum of all expansions:

-The Euclidian norm is the length of the vector as mentioned above:

-The sum norm is the sum of all expansions:

-Basically

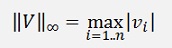
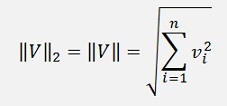
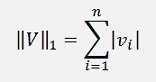
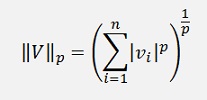
So take care with all this different kinds of norms :-)

Unit vector

The unit vector is a vector that just defines a direction. It’s length is 1. It is usually marked by a “^” over the character. The unit vector is quite useful in vector calculations. The unit vector to a given vector V is

Basic calculations

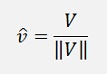
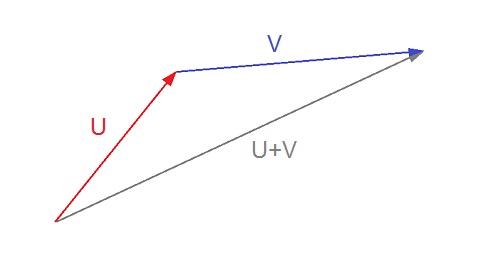
For illustration I use 3 dimensional vectors here. The definitions are the same fur multi-dimensional vectors (except for the cross product).

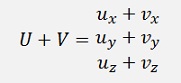
Addition of two vectors

To add 2 vectors means to add each expansion in one coordinate axis to the expansion of the same coordinate of the other vector.

Geometrically that means the two vectors are placed one on the other.

Subtraction of a vector from another vector

To subtract a vector from another is similar to the addition: Each expansion of one coordinate axis of the second vector is subtracted from the expansion of the same coordinate of the first vector.

That means geometrically –V is added to U.

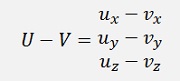
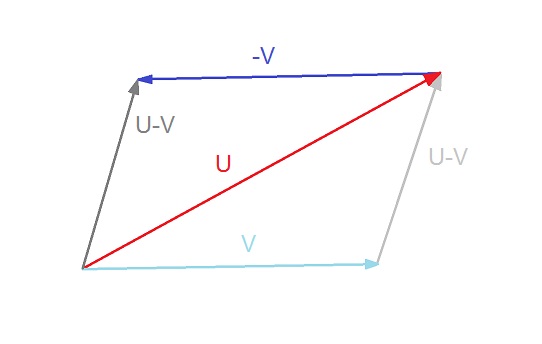
The resulting vector is the dark grey vector U - V. The light grey vector shows the distance vector between U and V. That means the distance between U and V can be calculated by subtracting V from U and then calculating the length of the resulting vector.

An application of vector additions is the superposition of speeds. If for instance an air plane flies from New York to Zurich and there is a strong jet stream blowing, the speed of the wind and the flying speed of the air plane in the air is add together and that gives the speed over ground.

Multiplication of a vector by a scalar

For the multiplication of a vector by a scalar each expansion is multiplied by the scalar.

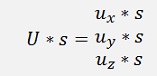
That’s just a stretching or shortening of the vector while it's direction remains the same.

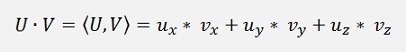
Multiplication of two vectors

If it comes to the multiplication of two vectors the situation becomes a little more complicate. There are 2 kinds of multiplications of vectors.

Dot product

The first one is called the inner product, dot product or scalar product. It has a scalar as output and is basically the lengths of both vectors multiplied and the result of this multiplied by the cosine of the angle between these vectors. Mathematically it’s:

Or in multidimensional spaces:

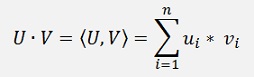
There are several different ways to write the dot product. It can be a dot like U∙V or brackets like

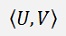
In some articles they use the dot product to calculate the length of a vector. Therefor the dot product of the vector with itself is built and the root is taken from that:

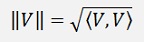
Others express the dot product as

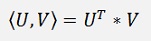
This is a matrix multiplication of the transposed of U by V. To transpose a vector of n dimensions lays it flat on a line and converts it to a matrix of one row and n columns. The multiplication of this by V is the same as computing the dot product of them.

Vector product

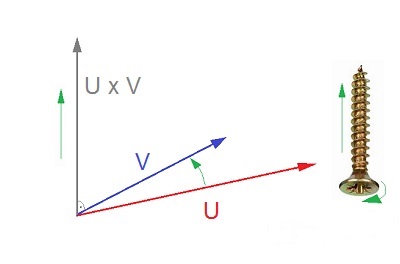
The second kind of multiplication is the vector product, cross product or outer product. This multiplication is defined only in 3 dimensional spaces and its result is a vector. The length of this vector is the product of the length of the multiplied vectors multiplied by the sine of the angle between these two vectors. Its direction is perpendicular to both vectors and it looks into the direction a screw moves if you turn it clockwise regarding the angle from first to second vector (hope you know how to tighten a screw :-)

That means if you have a vector product U x V and the both vectors are laying on a plane in front of you (virtually) turn the first vector towards the second and if this rotation is clockwise, the resulting vector looks away from you (the screw in the picture is turned clockwise and it moves upward. That’s the direction the resulting vector looks).

Mathematically U x V is:

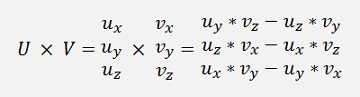
An application of the vector product is the calculation of the Lorenz force. If an electrically charged particle moves through a magnetic field it is exposed to the Lorenz force which is:

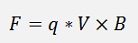
With F as the force vector, q the load of the particle, V the speed vector and B the magnetic field vector.

Another possibly more tangible application is the Coriolis force. See

https://en.wikipedia.org/wiki/Coriolis_force

To rotate a vector

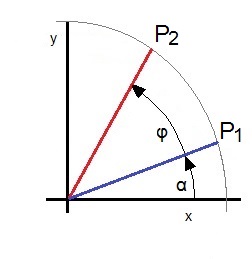
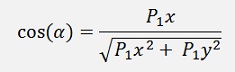
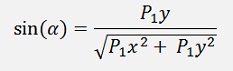
Just to add or subtract vectors or kind of multiply them is still not too interesting. I think vectors become attractive if they can be moved and an important part of the movement is rotation.If in 2 dimensional spaces a vector P₁ should be rotated by an angle φ to a vector P₂. That is:

There is

and

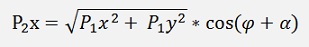
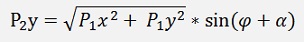
now

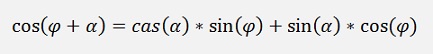
and with this:

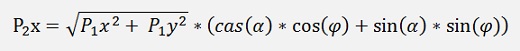
and with the equation for cos(α) and sin(α) from above:

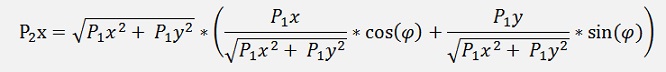
That can be simplified to

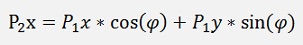
The same approach for p2y gives:

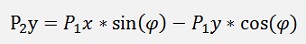
These two equations describe operations that can be expressed as one matrix multiplication

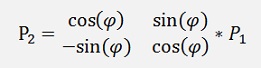
and the matrix

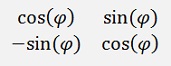
is a 2*2 rotation matrix.

If the vectors P₁ and P₂ would be 3 dimensional, the rotation matrix would be 3*3 too. Only, it would describe a rotation in one plane only. A vector with the dimensions x, y and z would be rotated by the angle α in the x-y plane by the rotation matrix:

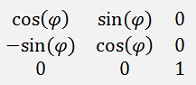
and the rotation matrix to rotate in the y-z plane would be:

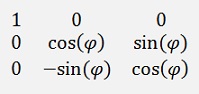
and for the x-z plane:

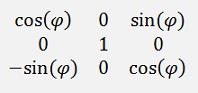
That’s the way to build a rotation matrix. For multi-dimensional spaces it’s basically the same. Only the matrix gets more columns and rows.

Maybe an interesting application is to draw an ellipse from a DXF definition. The DXF file format is a vector based format to define technical drawings in CAD and CAM. In this format an ellipse is defined by its position (x₀, y₀), the half axis A and B, a start angle (α₁), an end angle (α₂) and the inclination of its main axis (φ).

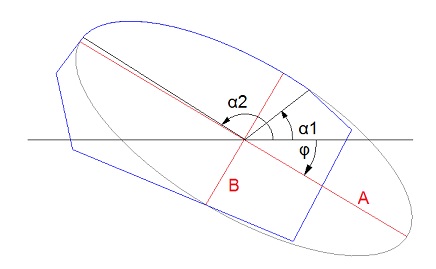
Ellipse segment embedded into a form (blue contour).

To draw this ellipse the equation for the centre point and the half axes:

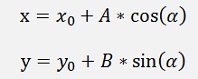
can be used.

Starting from α₁ and running to α₂ that draws the sector of an ellipse without an inclination. To include the inclination we just have to rotate the vector

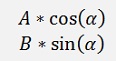
by the angle φ. That’s

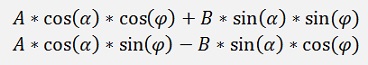
and calculate the points from α₁ to α₂ like

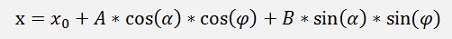
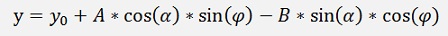
I implemented this in a small DXF file reader. Or better to say I extended the DXF sample of

https://www.codeproject.com/Articles/156522/DXF-Import-NET-Read-and-View-AutoCAD-Format-Files

to handle polylines, circles, ellipses and splines. O.k. I think it does not make too much sense to describe the DXF file format here. The interested reader might see at

https://www.autodesk.com/techpubs/autocad/acad2000/dxf/entities_section.htm

But the sample project, including some sample DXF files I found, is in the download link at the bottom of this article.

Some advanced vector calculations

For a AI-algorithm I recently faced the problem to set a perpendicular from a point V onto a line or a plane. I think that’s a good example to see that vectors can be quite cool :-)

Perpendicular from a point V onto a line

To set a perpendicular from a point V onto a line defined by 2 points P₁ and P₂ like:

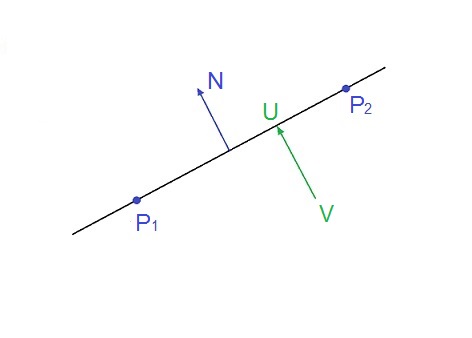
In the 3 dimensional space, the normal equation for a line

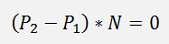
can be used.

With the normal vector N which is perpendicular to the line.

Now a vector U - V which is perpendicular should be found. Whereas U should lay on the line. That means

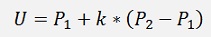
and

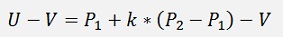
With k as a multiplication factor.

As U - V is perpendicular to the line:

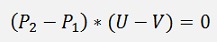
This is basically a scalar product like:

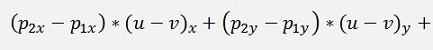
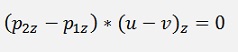
With the equation from above:

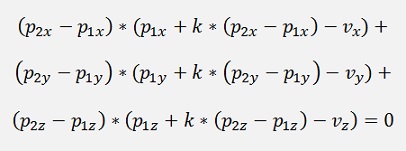
That can be resolved for k:

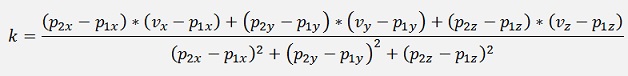
This used in

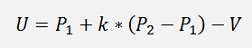
Gives the point U where the perpendicular comming from V meets the line. And the solution for k can easy be extended to more dimensional spaces. That’s really cool :-)

(Please note that U and V are principally points, but I interpret them as vectors here.)

Perpendicular from a point V onto a plane

To set a perpendicular from a point V onto a plane given by the equation:

In the 3 dimensional spaces.

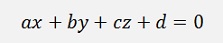
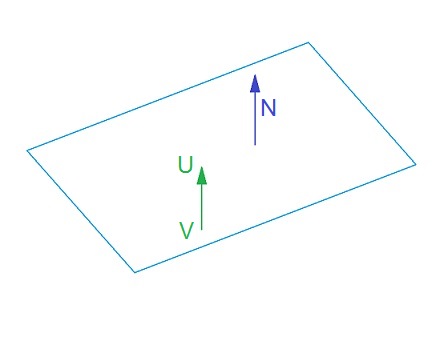
Is quite similar.

The point where the perpendicular meets the plane is U. This U shall be determined.

I use the unit vector of N which is perpendicular to the plane:

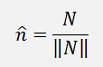
where

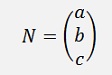
(from the above equation for the plane)

Whit this unit vector we can say

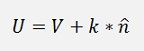
With k as a scalar factor.

U inserted into the equation for the plane gives

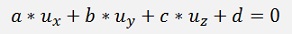
or the equation for U:

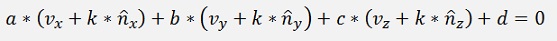
and this resolved for k:

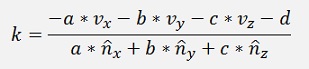
This k used in

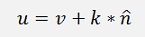
Gives the point U where the perpendicular starting at V meets the plane. Similar to the situation with the line the formula for k can easy be extended to more dimensional spaces as well :-)

C# Demo Project DXF file reader

DXF_File_Reader.zip