The Newton-Cotes formula is an algorithm to compute the definite integral of a given function f(x). It is based on the interpolation by Joseph-Louis Lagrange (See Lagrange interpolation for an introducition to the Lagrange interpolation) and its idea is to use the function f(x) to compute some supporting points, build the Lagrange polynomials to these supporting points and build the integral of these polynomials.
For the interpolation Lagrange calculates a weighting factor Lk to each supporting point like:
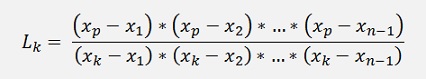
Where xp is the control variable for the interpolation and xn are the x coordinates of the supporting points. For the computation of the interpolation curve he multiplies each of these weighting factors by the y coordinate of its supporting point.
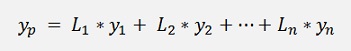
The formulation for the weighting factor can be written as:
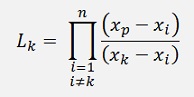
Now this interpolated curve can be integrated and that’s not too complicate.
The entire function
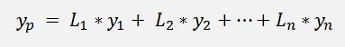
Can be split into parts and integrated like
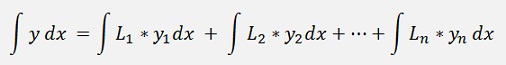
If we have a closer look at
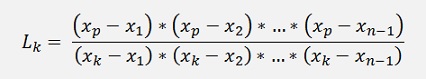
The denominator of this fraction is a polynomial of constant values. So for the integration it’s a constant value. The numerator is a polynomial in xp like:
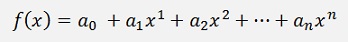
and that can easy be integrated as
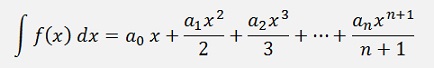
and if Lk is multiplied by yk. It is multiplied by a constant value as yk is a supporting point. That means
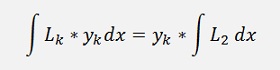
and
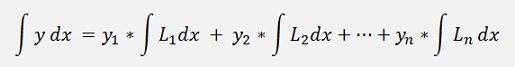
Now the Newton-Cotes formulation says to compute the integral from a to b:
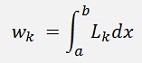
with k = 1 ... n
and the integral I is
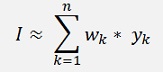
With wk as the integration weighting factor to the supporting point (xk, yk) and yk as the y value of a supporting point.
The formulation for the weighting factor is often written like:
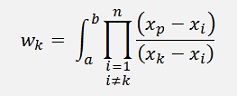
This formulation put into code looks like:
private double CalcWeights(int index)
{
int
i;
double res = 0;
double[] wl = new double[1];
double[] poly = new double[2];
wl[0] = 1;
// build polynomial
for (i = 0; i < x_k.Length; i++)
{
// build integral
res = wl[0]*(b-a);
for (i = 1; i < x_k.Length; i++)
{
return res;
} double res = 0;
double[] wl = new double[1];
double[] poly = new double[2];
wl[0] = 1;
// build polynomial
for (i = 0; i < x_k.Length; i++)
{
if
(i != index)
{
}{
poly[0]
=
-x_k[i] / (x_k[index] - x_k[i]);
poly[1] = 1 / (x_k[index] - x_k[i]);
wl = multPoly(wl, poly);
}poly[1] = 1 / (x_k[index] - x_k[i]);
wl = multPoly(wl, poly);
// build integral
res = wl[0]*(b-a);
for (i = 1; i < x_k.Length; i++)
{
res
= res
+ wl[i] * (Math.Pow(b,
i+1) - Math.Pow(a,
i+1)) / (i+1);
}return res;
This function computes the weighting factors for one supporting point in the array wl, buids the integral of all and returns this value in res. The multiplication of 2 polynomials is made in
private double[] multPoly(double[] p1, double[] p2)
{
int i, j;
double[] tempPoly = new double[p1.Length + p2.Length - 1];
for (i = 0; i < p1.Length; i++)
{
for (j = 0; j < p2.Length; j++)
{
tempPoly[j + i] = tempPoly[j + i] + p2[j] * p1[i];
}
}
return tempPoly;
}
With the supporting points in x_k and y_k and order as the number of supporting points the integral can be computed as:
integral = 0;
for (i = 0; i <= order; i++)
{
integral = integral + y_k[i] * CalcWeights(i);
}
And if the supporting points are calculated by a given function, this function is integrated.
As an interesting detail I regard the fact that the weighting factors are absolutely independent on the function itself. The y values of the supporting points in
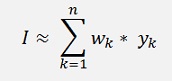
could be changed without influencing the wk values and the result would still be correct. That seems amazing


