A decision tree is an important algorithm in the field of machine learning. It is used to do classifications. This classifications are done by setting up a binary tree.
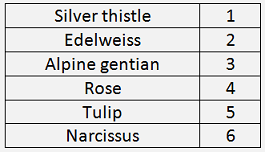
If we had some data of flowers like (that’s a constructed sample just for explanation
 ):
):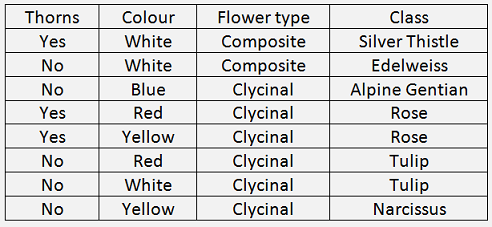
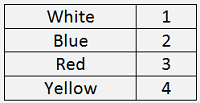
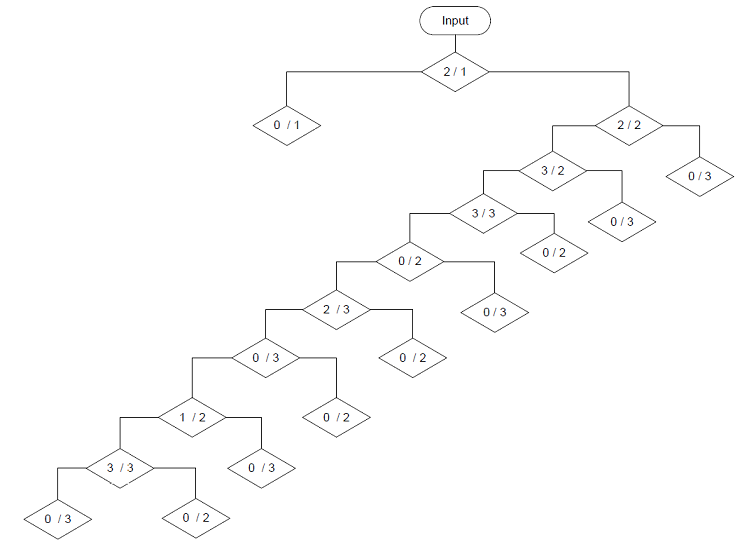
And we want to classify these flowers according to their properties in a binary tree without knowing the flower class, we would have to find properties to separate the flower classes as well as possible. In this sample data there is just one flower class that has the colour blue. So we could start with a first step by comparing the colour of each class to the colour blue. That would separate the class Alpine Gentian from all the other classes. For the remaining classes we could start a new branch and compare the flower type to the type composite. That would separate the classes Silver Thistle and Edelweiss from the others. For these two classes we can go on in another new branch by the property thorns. That separates the Silver Thistle from the Edelweiss and we would be done for this branch. And so on. The complete tree would look like:
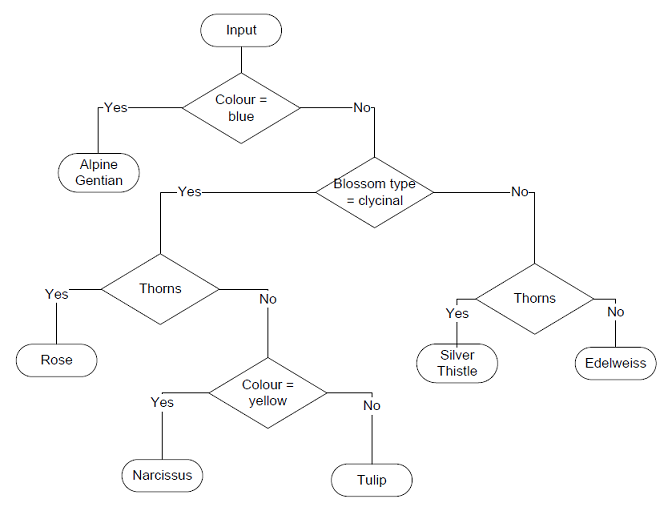
That was a simple example. If the data is more complex, the task becomes quite soon much more complicate and we have to let a computer do it by a clever algorithm and that’s the decision tree algorithm

To build such a tree in a computer algorithm the great question is how to find the one property that separates a class the best for each branch. One way to find this is to check how pure the separation is achieved by the use of a certain property and class. Therefore the Gini factor can be used. In the decision tree we always try to separate classes as complete as possible. So the approach is to start with one class. In the sample from above that was the class Alpine Gentian for the first iteration. And to this class we use the property colour and separate according to this property. This separation is already pure as we have the target class Alpine Gentian separated from all the other classes. If we would try to separate the Alpine Gentian according to the property flower type Clycinal that would separate the classes Rose, Tulip and Narcissus as well. So the separation is not very pure. The gini factor is a measurement of the purity of the separation.
The basic formulation for the gini factor is:
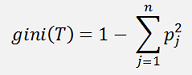
Where p is the probability of the target class to be separated and for the other classes not to be separated. And T stands for a lot of samples. This formula means basically gini is the sum of the number of samples of a class on its side of the branch divided by the number of samples brought into this branch.
In the sample above that is for the top branch.
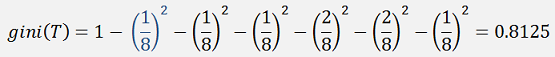
The first (blue) fraction is the probability of the target class Alpine Gentian. 1 sample of 8 has been separated. The other fractions are for 1 Silver Thistle, 1 Edelweiss, 2 Roses, 2 Tulips and 1 Narcissus which are all on the other side of the separation.
If we would separate the target class Alpine Gentian by the property flower type Clycinal. That would give:
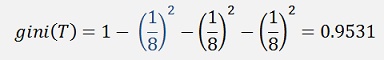
The blue fraction again for the Alpine Gentian that was separated correctly and the other 2 fractions for 1 Silver Thistle, 1 Edelweiss. All the others are not separated correct and are therefore neglected (note that the not correct separated samples will be placed on the left side of the branch).The smaller the gini the purer and therefore better is the separation. So the task is to find the class and property to separate the classes yielding the smallest gini factor for one crotch of a branch (at least for a first approach
 ). And if this best combination is found,
separate the samples with this property and use these 2 lots of samples
to do the same again and repeat until there are only single classes
remaining in the separated lots and the algorithm has reached the
leaves of the branches. Sounds easy
). And if this best combination is found,
separate the samples with this property and use these 2 lots of samples
to do the same again and repeat until there are only single classes
remaining in the separated lots and the algorithm has reached the
leaves of the branches. Sounds easy 
For the separation I search for the minimum and maximum value of the selected property of the selected class and do the separation with these. That takes all members of the selected class and put them into a new data set for the following branch to the left. For the following branch to the right I collect all the members that lay outside of this minimum and maximum and put them into a new data set. All the other samples that can not be separated like this I add to the data set of the target class samples. With these two data sets I calculate the gini factor and if the combination with the smallest gini factor is found these two new data sets are used to call the function BuildBranch 2 times recursively to build the following branches. In case the right data set is empty, the following branch on the left side will be a leave and will have a gini factor of 0. That means recursion has got to an end for this branch.
In a recursive function that builds these branches that looks like:
private void BuildBranch(ref TBranch actBranch, Collection<double[]> values)
{
int iActClass, iActProperty, j;
for (iActClass = minClass; iActClass <= maxClass; iActClass++)
{
for (iActProperty = 0; iActProperty < features; iActProperty++)
{
TBranch branch = new TBranch();
CalcGini(iActClass, iActProperty, branch, values);
if (actBranch.gini > branch.gini)
{
actBranch.purity = branch.purity;
actBranch.iProperty = branch.iProperty;
actBranch.iclass = branch.iclass;
actBranch.max = branch.max;
actBranch.min = branch.min;
//actBranch.localValues = values; Just for debugging
if (actBranch.purity > 0) // if gini == o there is only one class remaining
{
Collection<double[]> nextValuesL = new Collection<double[]>();
Collection<double[]> nextValuesR = new Collection<double[]>();
for (j = 0; j < values.Count; j++)
{
if ((values.ElementAt(j)[actBranch.iProperty] <= actBranch.max) && (values.ElementAt(j)[actBranch.iProperty] >= actBranch.min))
nextValuesL.Add(values.ElementAt(j));
else
nextValuesR.Add(values.ElementAt(j));
}
if (nextValuesL.Count > 0)
{
actBranch.nextBranch[0] = new TBranch();
BuildBranch(ref actBranch.nextBranch[0], nextValuesL);
}
if (nextValuesR.Count > 0)
{
actBranch.nextBranch[1] = new TBranch();
BuildBranch(ref actBranch.nextBranch[1], nextValuesR);
}
}
}
}
}
}
With
private void CalcGini(int iClass, int iProperty, TBranch branch, Collection<double[]> values)
{
bool foundClass = false;
bool othersEmpty = true;
double classMin = 1e50;
double classMax = -1e50;
double gini;
int[] iOthersCount = new int[nbOfClasses-1];
int[] iOthersClass = new int[nbOfClasses-1];
int iActIndex = 0;
int iClassCount = 0;
int i, j;
for (i = 0; i < iOthersClass.Length; i++)
iOthersClass[i] = -1;
for (i = 0; i < values.Count; i++)
{
if (values.ElementAt(i)[dataLength - 1] == iClass)
{
foundClass = true;
if (values.ElementAt(i)[iProperty] < classMin)
classMin = values.ElementAt(i)[iProperty];
if (values.ElementAt(i)[iProperty] > classMax)
classMax = values.ElementAt(i)[iProperty];
}
}
if (foundClass)
{
for (i = 0; i < values.Count; i++)
{
if (values.ElementAt(i)[dataLength - 1] != iClass)
{
if ((values.ElementAt(i)[iProperty] > classMax) || (values.ElementAt(i)[iProperty] < classMin))
{
foundClass = false;
for (j = 0; j < iOthersClass.Length; j++)
{
if (iOthersClass[j] == (int)values.ElementAt(i)[dataLength - 1])
foundClass = true;
}
if(!foundClass)
{
iOthersClass[iActIndex] = (int)values.ElementAt(i)[dataLength - 1];
iActIndex++;
}
for (j = 0; j < iOthersClass.Length; j++)
{
if (iOthersClass[j] == (int)values.ElementAt(i)[dataLength - 1])
iOthersCount[j]++;
}
}
}
else
iClassCount++;
}
for (j = 0; j < iOthersClass.Length; j++)
{
if (iOthersCount[j] != 0)
othersEmpty = false;
}
if ((!othersEmpty) || (iClassCount == values.Count))
{
gini = 1.0 - (iClassCount / values.Count) * (iClassCount / values.Count);
for (i = 0; i < iOthersClass.Length; i++)
gini = gini - (iOthersCount[i] / values.Count) * (iOthersCount[i] / values.Count);
branch.purity = gini;
branch.min = classMin;
branch.max = classMax;
branch.iclass = iClass;
branch.iProperty = iProperty;
}
else
branch.purity = USELESSLEAVE;
}
else
branch.purity = USELESSLEAVE;
}
The function BuildBranch(..) called like:
BuildBranch(ref trunc,
data.values);
And as the algorithm works with numbers and not wit strings, I substituted the properties like:

That builds exactly the tree as drawn above
 .
.It runs in 2 loops through all the properties and classes, calculates the gini-factor and keeps the combination with the smallest gini to go on with two recursive calls.
At the end there is a tree of instances of the class
public class TBranch
{
public double min;
public double max;
public double purity;
public int iclass;
public int iProperty;
public TBranch[] nextBranch;
public Collection<double[]> localValues;
public TBranch()
{
nextBranch = new TBranch[2];
purity = 100;
}
public int CheckBranch(double[] data)
{
int result = -1;
if (purity == 0)
{
if ((data[iProperty] <= max) && (data[iProperty] >= min))
result = iclass;
else
{
if (nextBranch[0] != null)
result = nextBranch[0].CheckBranch(data);
}
}
else
{
if ((data[iProperty] <= max) && (data[iProperty] >= min) && (nextBranch[0] != null))
result = nextBranch[0].CheckBranch(data);
else
{
if ((nextBranch[1] != null) && result < 0)
result = nextBranch[1].CheckBranch(data);
}
}
return result;
}
}
The function CheckBranch(..) is used to run through the finished tree with one sample and to classify it.
The C# demo project at the very bottom of this article does this all. It creates the tree, classifies the 8 data samples and lists the result in a DataGridView.
For a bit a more complex and realistic example I used the Iris data set once more and applied this algorithm to it. I extended the demo project from above by a function to save the tree in a XML structure from where it can be reloaded by the test project. Similar to how I did for the backpropagation algorithm I split the set into a training and a test data set of 135 and 15 samples.
With this training data the algorithm creates this tree:
With property / class combination for the smallest gini in each romb or crotch. In the test application this tree is used to classify the 15 test data samples.
The result is:
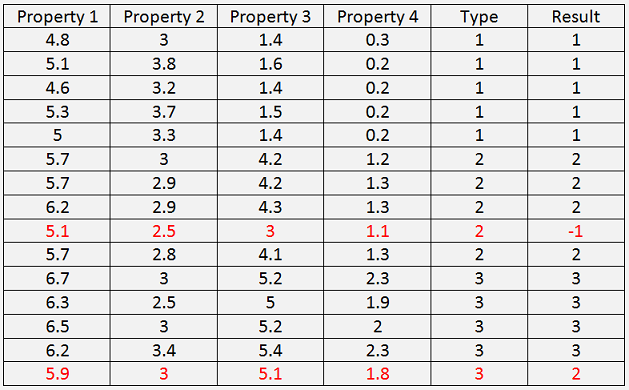
Not all test samples are classified correct. The fourth sample of the Iris-versicolor cannot be classified at all and shows -1. If we look at the minimum and maximum values of the 4 properties of Iris-versicolor, its:

Property 1, 2 and 4 of this not classified sample fit into these limits, but property 3 is outside and this sample can therefore not be classified as Iris-versicolor and in both other classes it does not fit as well.
The last test sample fits not only into the limits of Iris-virginica:

but also into all limits of Iris-versicolor and unfortunately therefore is unfortunately classified wrong. That shows a little weakness of this algorithm. If some properties would basically fit to a certain class because of their values, but they are within the limits of another class, that can lead the algorithm to a wrong decision

O.k. the Iris data set is possibly not the best data set to implement a decision tree

To use just the gini factor of the actual branch is a rather simple approach and might work quite well. But if a better solution is required, an a bit more complex approach to build the tree is needed and for this not only the gini factor of the actual crotch of a branch should be taken into account, but also the gini factors of all following branches. That means we do not just look for one minimum gini factor and go on, but compute the gini factor of one combination of property and class, run through all the possible following branches and search for the minimum gini factor for these branches, including all the following gini factors as well and search for the minimum of the resulting gini factor of all these. The formulation for the building of this resulting gini factor is:
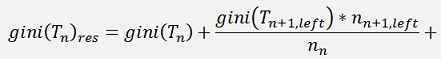
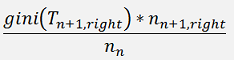
For one crotch n of a branch the gini of the set (Tn)res is the sum of the gini of this crotch and the gini factor of the following branches divided by the number of samples in the actual crotch, multiplied by the number of samples in particular following crotch.That means the algorithm has to run down and up the tree many times. That consumes a lot of computation time. Therefore it makes sense to implement some limitations. One limitation is to stop the recursions if a certain deepness is reached. In the upper approach a tree was built that was 10 crotches deep. So I limited the number of recursions to 10. This limitation does not only reduce calculation time, it's a good method to prevent from overfitting. Another limitation is to skip the further recursion if we have already computed a gini factor and the newly computed gini factor is bigger even without the adding of the ginis of the following branches. With these limitations the BuildBranch(..) function looks like:
private double BuildBranch(ref TBranch actBranch, Collection<double[]> values)
{
int iActClass, iActProperty, j;
double localGiniL = 0;
double localGiniR = 0;
if (nbOfRecs <= MAXRECURSIONS)
{
for (iActClass = minClass; iActClass <= maxClass; iActClass++)
{
for (iActProperty = 0; iActProperty < features; iActProperty++)
{
TBranch branch = new TBranch();
calcGini(iActClass, iActProperty, branch, values);
if ((branch.purity > 0) && (branch.purity < actBranch.purity))
{
Collection<double[]> nextValuesL = new Collection<double[]>();
Collection<double[]> nextValuesR = new Collection<double[]>();
for (j = 0; j < values.Count; j++)
{
if ((values.ElementAt(j)[branch.iProperty] <= branch.max) && (values.ElementAt(j)[branch.iProperty] >= branch.min))
nextValuesL.Add(values.ElementAt(j));
else
nextValuesR.Add(values.ElementAt(j));
}
nbOfRecs++;
if (maxRecs < nbOfRecs)
maxRecs = nbOfRecs;
if (nextValuesL.Count > 0)
{
branch.nextBranch[0] = new TBranch();
localGiniL = BuildBranch(ref branch.nextBranch[0], nextValuesL) * nextValuesL.Count;
}
if (nextValuesR.Count > 0)
{
branch.nextBranch[1] = new TBranch();
localGiniR = BuildBranch(ref branch.nextBranch[1], nextValuesR) * nextValuesR.Count;
}
nbOfRecs--;
}
branch.purity = branch.purity + (localGiniL + localGiniR) / values.Count;
if (actBranch.purity > branch.purity)
{
actBranch = branch;
}
if (actBranch.purity == 0)
{
iProperty = features;
iActClass = maxClass + 1;
}
}
}
}
else
actBranch.purity = USELESSLEAVE;
return actBranch.purity;
}
It returns the local computed gini factor and must be called like:
BuildBranch(ref trunc, data.values);
And that builds the tree
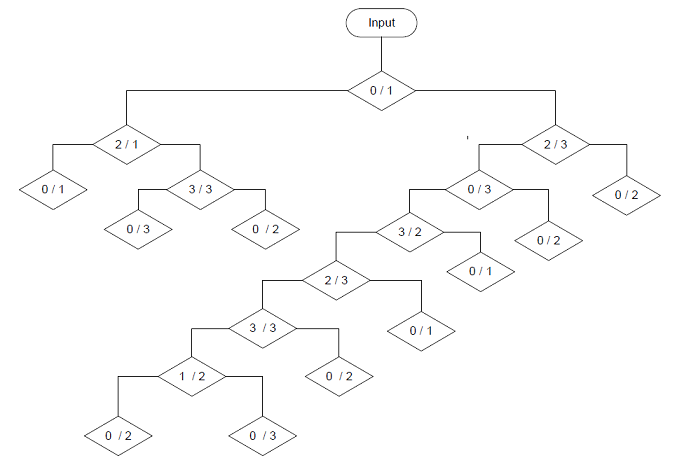
It has a deepness of 8 crotches and looks a bit more compact than the one above. That’s quite an improvement

And the result with the test data is a little better. 14 of the 15 test samples are classified correct. But still not all sample are classified correct.
Another possibility to improve the algorithm is to use the Entropy instead of the Gini factor to determine the purity of the separation. The formulation for the Entropy is:
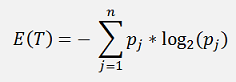
Using the Entropy gives a bit a more balanced tree.
For this the lines
gini = 1.0 - (iClassCount / values.Count) * (iClassCount / values.Count);
for (i = 0; i < iOthersClass.Length; i++)
gini = gini - (iOthersCount[i] / values.Count) * (iOthersCount[i] / values.Count);
In the function CalcGini() must be replaced by
p = (double)iClassCount / (double)values.Count;
entropy = -p * Math.Log(p) / ln_2;
for (i = 0; i < iOthersClass.Length; i++)
{
if (iOthersCount[i] > 0)
}p = (double)iOthersCount[i] / (double)values.Count;
entropy = entropy - p * Math.Log(p) / ln_2;with
double ln_2 = Math.Log(2);
double entropy, p;
double entropy, p;
and using this Entropy as purity gives the tree.
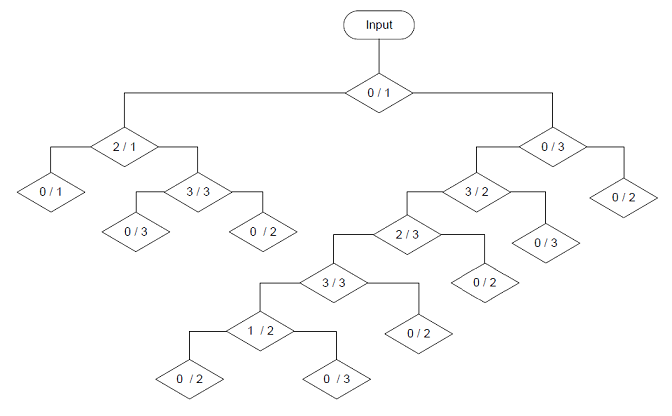
Again there is an improvement in the deepness of the tree. But there is also a disadvantage. The computation of the logarithm is quite time consuming and therefore the building of the tree takes much longer. For a small tree like the one here that doesn’t matter too much. But if the tree becomes big, it’s makes quite a difference.
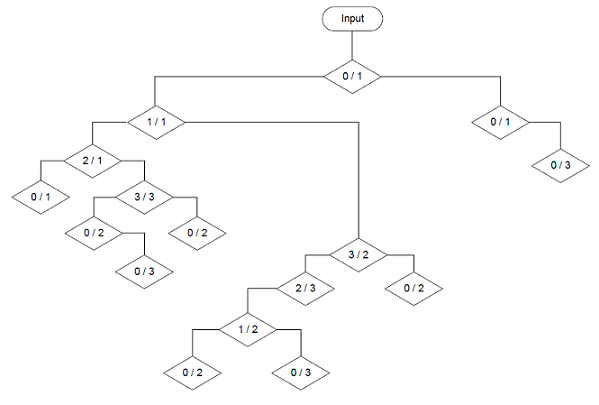
Now, there is still a possibility to optimize this tree. Reducing the maximal depth of the tree forces the algorithm to find a more balanced solution. This limitation can be achieved by reducing the max number of recursions. For a first try I set the max recursions to 10 and that produced a tree with a depth of 6 branches. So reducing the max recursions down to 6 does not change anything as the depth is 6 branches already. But reducing the max recursions to 5 changes the structure of the tree quite a bit.
With this using the gini factor builds .
And using the Entropy.
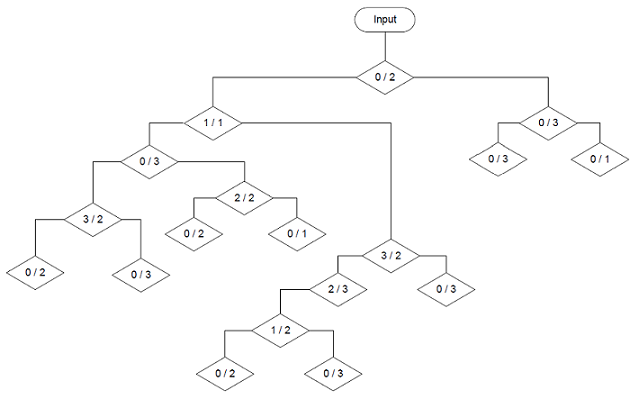
Both trees have a maximum depth of 5 branches now. Interesting to see how this reforms the tree

The result with the test data is still the same: One test sample is not correct classified.
The decision tree seems not to be the best joyce to classify the Iris data (see Classifying data by a Support Vector Machine for a better solution
 )
)
To save the tree structure and reload it in the test application I add the two functions:
public XElement writeBranch(int index)
{
XElement xmlBranch = new XElement("Branch", index);
xmlBranch.Add(new XAttribute("Class", iclass));
xmlBranch.Add(new XAttribute("Gini", gini));
xmlBranch.Add(new XAttribute("Min", min));
xmlBranch.Add(new XAttribute("Max", max));
xmlBranch.Add(new XAttribute("Property", iProperty));
if (nextBranch[0] != null)
{
xmlBranch.Add(nextBranch[0].writeBranch(0));
}
if (nextBranch[1] != null)
{
xmlBranch.Add(nextBranch[1].writeBranch(1));
}
return xmlBranch;
}
and
public XElement loadBranch(XElement xmlBranch)
{
iclass = Convert.ToInt32(xmlBranch.Attribute("Class").Value);
purity = Convert.ToDouble(xmlBranch.Attribute("Gini").Value);
min = Convert.ToDouble(xmlBranch.Attribute("Min").Value);
max = Convert.ToDouble(xmlBranch.Attribute("Max").Value);
iProperty = Convert.ToInt32(xmlBranch. Attribute ("Property").Value);
IEnumerable subChields = xmlBranch.Elements("Branch");
if (subChields != null)
{
foreach (XElement subelement in subChields)
{
int index = Convert.ToInt32(subelement.FirstNode.ToString());
if ((index >= 0) && (index < nextBranch.Length))
{
nextBranch[index] = new TBranch();
nextBranch[index].loadBranch(subelement);
}
}
}
return xmlBranch;
}
Both are recursive functions that save and load a random tree structure.
To save the structure the writeBrach() function can be called like:
XDocument doc = new XDocument();
doc.Add(new XElement("Treesetting", null));
using (XmlWriter writer = XmlWriter.Create(FileName))
{
doc.Root.Add(branch.writeBranch(0));
doc.WriteTo(writer);
}
And to load it
XElement doc = XElement.Load(FileName);
IEnumerable chields = doc.Elements("Branch");
foreach (XElement el in chields)
{
branch.loadBranch(el);
}
The demo project consists of one main window:
This window shows the data with its 4 properties and the flower type as number 1 to 3 and in the output row the classified flower type is listed. After building the tree the application runs through all data samples and classifies them with the built tree for checking the correctness of the tree and lists them in the column "output". The tree structure is saved into the XML file “setup.xml” this file must be copied into the application directory of the test application to classify the 15 test samples.

