Gerolamo Cardano published a method to solve a cubic equation in 1545. There is a description of this method on Wikipedia. But it is not too detailed and on the German Wikipedia even the last part is missing and so it’s impossible to implement a working algorithm by the aid of this. So I thought I try to do a more detailed explanation

The method of Cardano is based on the reduction of the equation polynomia
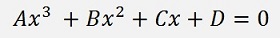
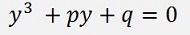
First of all the entire equation is divided by A to get the form
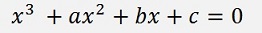
Now Cardano makes a variable substitution and replaces x by the term y + α. With this the equation becomes:
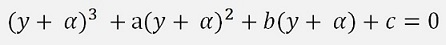
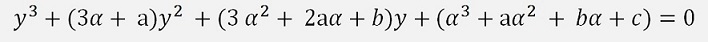
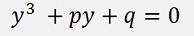

Now there is another substitution: y will be substituted by u + v and we get
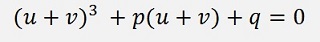
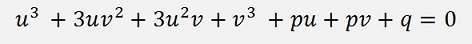
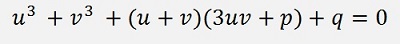
This condition for q we put into square now and the one for p divided by 3 to the power of 3 and multiply it by 4.
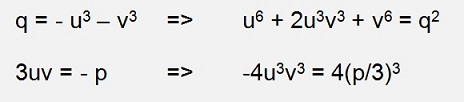
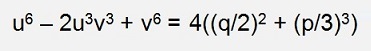



y = u + v
and (not to be forgotten
 )
)x = y – a/3 = u + v – a/3
As we are looking for x and not for y.
Now there are the 3 possibilities D >= 0 , D = 0 and D < 0:

As the cubic root of a real number can have two complex solutions. One at the complex angle of 120° and the other one at 240°. The two complex solutions are of the same length as u0 and v0, but one has the complex angle 120° and the other one 240°. That means with



 .
.Further above we had the clause u*v = - p/3 and this is not the case for all 9 combinations of u and v. Principally it’s valid for the u0 * v0, u1 * v2 and u2 * v1. Let’s have look at u1 * v2. That’s

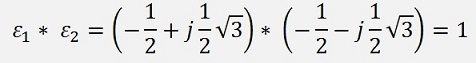
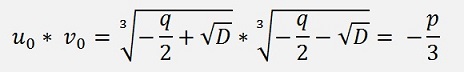
y1 = u0 + v0
y2 = u1 + v2
y3 = u2 + v1
(and don’t forget x = y – a/3
 )
)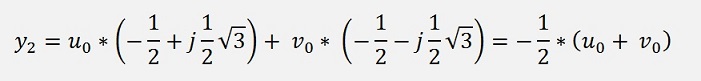
y1 = u0 + v0
y2 = -(u0 + v0)/2

With the substitution from further above
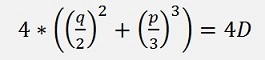
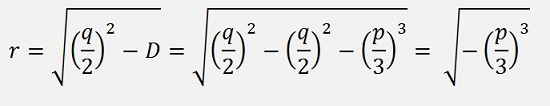
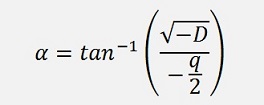
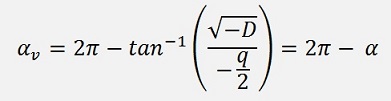
 . The cubic root of a complex
number has not just 1 but 3 solutions. The angle α we get
once by multiplying α/3 by 3, twice by multiplying (2π
+ α)/3 by 3 and thirdly by multiplying (4π +
α)/3 by 3. That makes 3 solutions for u and 3 solutions for
v. They look like:
. The cubic root of a complex
number has not just 1 but 3 solutions. The angle α we get
once by multiplying α/3 by 3, twice by multiplying (2π
+ α)/3 by 3 and thirdly by multiplying (4π +
α)/3 by 3. That makes 3 solutions for u and 3 solutions for
v. They look like: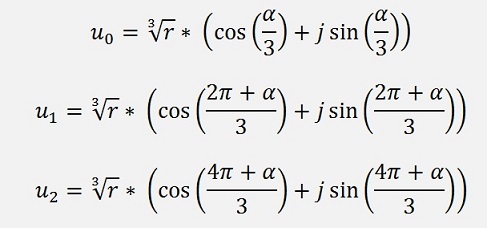
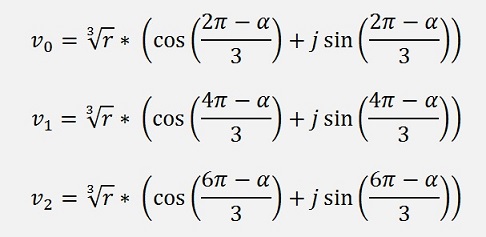
u0 + v2
u1 + v1
u2 + v0
the imaginary part becomes 0 and the solutions are
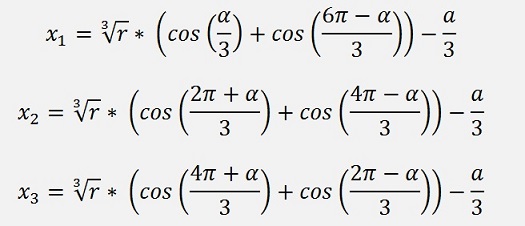

There is a small online solver in JavaScript for this on Cardano solver).

