In a facebook group for Mathematics I recently saw a question about the calculation of limit values. The determination of such limit values is often used in differential calculus (See Differential calculus) and expansion in series.
The word limes comes from Latin and means something like a border wall and the expression
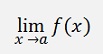
Means the limiting value of f(x) if x approaches a. Usually f(a) is infinite or undefined but if x is very close to a f(x) still has valid output and can be determined.
There are different situations for these limit calculations. Sometimes the limit must be determined for a value running to infinity, sometimes the value should run towards 0 and sometimes it should run to a random value.
So the usual approach is to bring the expression into a form where the limit value does not influence that bad anymore. This can be achieved by various mathematical operations. Principally, for a limiting value towards infinity, the goal is to get the expression into a for where x is in fractions in the denominator. So the fraction becomes 0 if x becomes infinite.
For a limiting value towards 0 we should end with a fraction where x is in linear form and raised to various powers. Then we can say that x2 approaches 0 much faster than x and higher powers of x even faster. So all the higher powers of x can be neglected and only x remains if x gets very close to 0.
If the following expression should be evaluated:
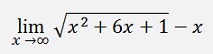
A first step is to extend the whole thing by
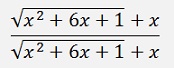
That’s
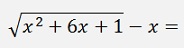
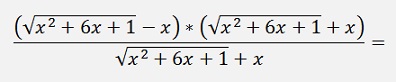
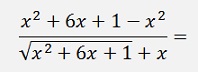
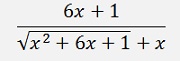
Then enumerator and denominator are divided by x2:
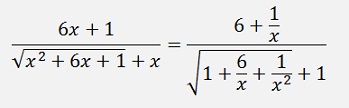
If x approaches infinity now, all the fractions with x in the denominator become 0 and we get:
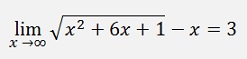
Another sample is an expression where x runs towards a given value.
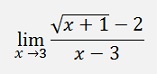
In such cases I often use a simple Excel sheet to get a first idea where the value goes. I just enter the value running towards its limit int one column and the expression in the nest on (sorry for the German “Wurzel”. That means “Root”
 )
)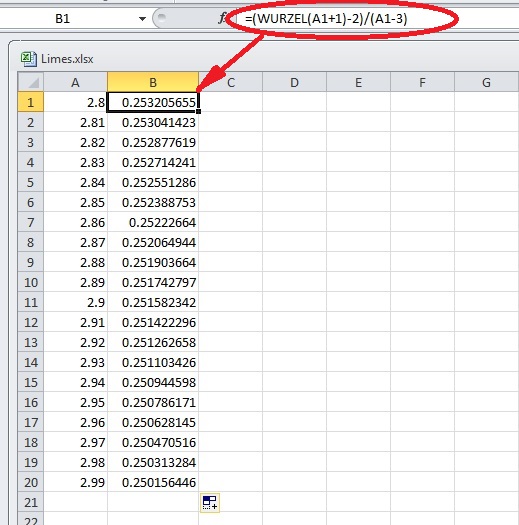
With this I see the outcome of the expression runs towards 0.25 if x approaches 3.
Now let’s see how to get that formal:
I extend the expression by
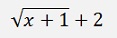
That’s:
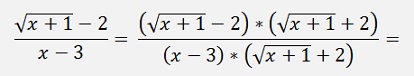
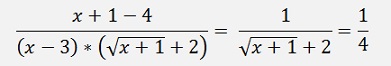
That’s: it

Another interesting sample is
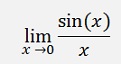
That requires another approach. On possibility is to write the sinus function as a
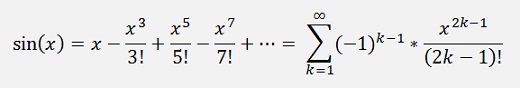
If x becomes very small x3 approaches 0 much quicker then x and x5 even faster…and so on. Whit that all the powers of x can be neglected and:
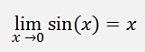
and
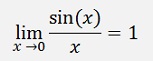
Another approach is
De l,Hospital says if f(a) = 0 and g(a) = 0, then
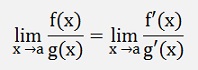
This is based on the mean value theorem of the differential calculus that says:
If a > b and x >= b and x <= a and f(x) can be differentiated, there exists an x with
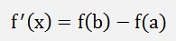
That means no matter how f(x) is bent, there is a place between a and b where the differentiation f’(x) = f(b) – f(a).
Now, if a = x0 and f(x0) = 0 and b approaches x0 , x must approach x0 to and we get
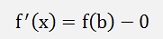
and
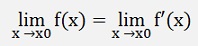
and with this
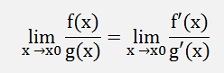
This can be used to determine
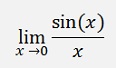
Here both, enumerator and denominator become 0 if x becomes 0 and so the theorem of De l’Hospital can be used:
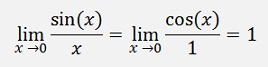
Another interesting sample is
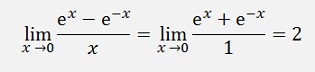
It’s also solved by the usage of De l’Hospital


