When it comes to matrix calculations, most of my colleagues say: “Uuuh. Ugly! Terrible” I say that’s not fair (o.k. you might take me as a fool now
). Matrix calculations are
quite cool. Have a look in (see Rotation Matrix
or even Householder
transformation.
A Householder transformation: That’s fine art of matrix
calculations )A matrix is a field of numbers containing n rows and m columns. The number of rows can differ from the number of columns. If they are equal, the matrix is a square matrix (for instance a 4*4 matrix like here).
Each matrix has a so called main diagonal consisting of the elements aii. If the matrix is not a square matrix this main diagonal does not lead from edge to edge. But that should not bother
A 4 * 4 matrix with the main diagonal elements marked red looks like this:
A square matrix can be symmetrical. That means the values symmetrical to the main diagonal are equal.
That’s quite an interesting point for various manipulations and occurs quite often.
A 4 * 4 matrix with the main diagonal elements marked red looks like this:
A matrix that has only in the main diagonal elements that are not 0 is a diagonal matrix:
A matrix that has in its main diagonal and each element to the left and right of the diagonal element values not 0 is a tridiagonal matrix.
A matrix can be mirrored at its main diagonal. Such a matrix is called transposed matrix AT (see Transposed Matrix)
AT would look like:
Transposing a not square matrix switches the number of rows and columns.
Transposed matrixes have some importance in some algorithms (see Method of the least squares) and are therefore quite interesting.
As matrixes are not simple numbers, there are special regulations for matrix calculations:
The addition of two matrixes A+B is quite simple: Each element of A is added to the same element of B:
For the multiplication of two matrixes A * B there is the rule to lay the rows of A on the columns of B. That means we take a row of A and a column of B. Multiply the first elements of these, the second elements, the third and so on and finally add results of these multiplications together. That is the resulting element of the same row and column in the result matrix. If we multiply two 4*4 matrixes
The elements of the first row of C will be:
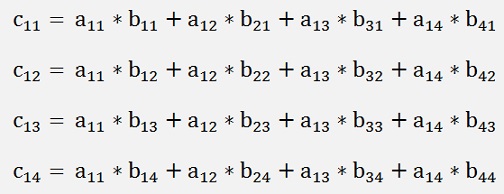
The second row:
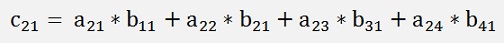
And so on.
And the entire multiplication is:
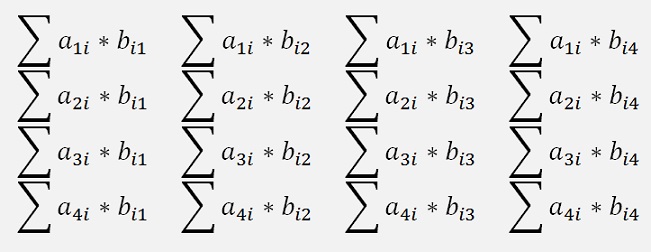
That means there is the limitation that the left side matrix of the multiplication must have the same number of columns as the right side matrix has rows. Otherwise the multiplication is not possible. We can multiply a n*n matrix by a n dimensional vector. But the vector must be on the right side.
That means The matrixes or vectors of a multiplication cannot be switched.
Even if the multiplication would be possible, the result would not be the same if the matrixes would be switched. That’s an important fact.
Orthogonal and orthonormal matrixes
Orthogonal and orthonormal matrixes have the special characteristic that their column vectors are orthogonal one to the other. That means the dot product of two such vectors is 0. For example the dot product of the first 2 vectors of a 4*4 matrix
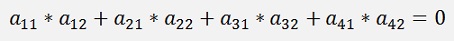
The orthonormal matrix additionally has the characteristic that the length of its column vectors is 1. That means the column vectors are normalized. These characteristics bring some additional topics.
The multiplication of an orthogonal and orthonormal matrix with its transposed matrix yields a diagonal matrix. If the matrix is orthonormal, the resulting diagonal matrix is the identity matrix.
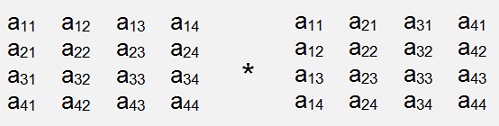
With my favorited 4*4 matrix
A * AT
=
=
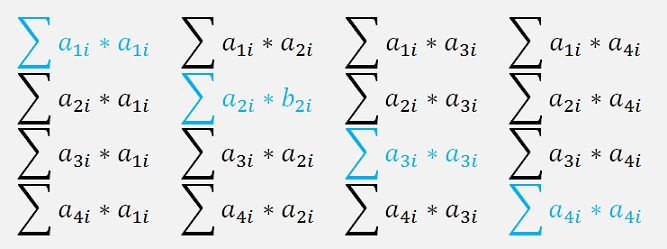
All the sums that are not in the main diagonal are dot products of two different vectors and because of the orthogonality 0. Only the diagonal elements become not 0. Only the diagonal elements are not 0. With the orthogonal matrix they contain the square of the length of the corresponding column vector and with the orthonormal matrix they are all 1. That means the multiplication of a orthonormal matrix with its transposed yields the identity matrix.
A funny detail is that we get the same result if we change the order of the multipliers:
Now the fact that for an orthonormal matrix A * AT = I is quite an interesting thing. As the multiplication of the identity matrix by another matrix B does not change anything on B.
An orthonormal matrix Q can be eliminated on one side of an equation like:
This can be extended by QT.
and that is
or
That’s quite helpful in some cases. I used that in me algorithm for the method of the least squares (see The method of the least squares).
Buth don’t forget: That’s valid only for orthonormal matrixes