Reinsch Algorithm

In the 2. Order Goertzel algorithm the factor a1 = -2 cos(2kπ/N) is used in the main loop in every cycle. With a great number of data samples N becomes quite great and therefore a1 quite close to -2. On a computer this can lead to round off errors and due to that to instability of the algorithm.

The Reinsch algorithm is a modified Görtzel algorithm that should run more stable than the 2. order Goertzel algorithm.

In the description to the 2. order Goertzel Algorithm we found the signal path

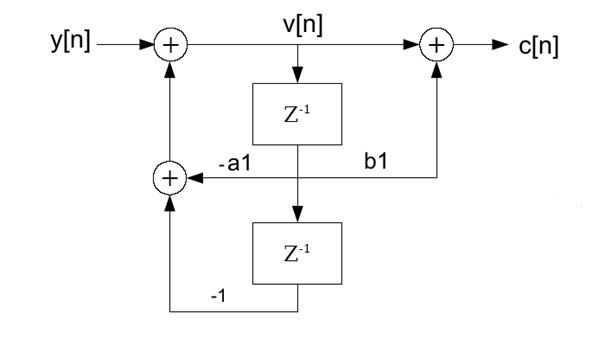
And the formula to implement it as v[n] = y[n] – a1 * v[n-1] – v[n-2]

for the feedback part

and

c[n] = v[n] + b1 * v[n-1]

for the feed forward part.

with

a1 = -2 cos(2kπ/N) and b1 = -exp(-j2kπ/N)

Reinsch took this formulas and distinguished 2 cases:

cos(2Pi*k/N) > 0 and cos(2Pi*k/N) >= 0

Case cos(2Pi*k/N) > 0

For cos(2Pi*k/N) > 0 Reinsch takes the part

v[n] = y[n] - a1 * v[n-1] - v[n-2]

Reinsch just extends both sides of this equation by – v[n-1] and says for the difference between v[n] – v[n-1]

v[n] - v[n-1] = y[n] - a1 * v[n-1] - v[n-2] - v[n-1]

then he expands this equation by +2 * v[n-1] and – 2 * v[n-1] and as a1 = -2cos(2Pi*k/N), he gets

v[n] - v[n-1] = y[n] + (2cos(2Pi*k/N) - 2) * v[n-1] + v[n-1] - v[n-2]

Now there are two substitutions:

(2cos(2Pi*k/N) - 2) = - 4 * sin(Pi*k/N)^2

And with v[n] – v[n-1] = dv[n], the last two terms v[n-1] – v[n-2] = dv[n-1],

we get:

dv[n] = y[n] - 4 * sin(Pi*k/N)^2* v[n-1] + dv[n-1]

and finally for v[n]:

v[n] = dv[n] + v[n-1]

This is a loop with dv[n] as feedback part and looks like:

a1.real = -4 * Math.Pow(Math.Sin((double)(Math.PI * (double)(k) / (double)(N))), 2.0);
a1.imag = 0;
we[k].real = a1.real;
for (n = 0; n < N; n++)
{
      dW = y[n].real + a1.real * v1.real + dW;
      v0.real = dW + v1.real;
      v1 = v0;
}
c[k].real = (dW - a1.real / 2.0 * v0.real) / (double)(N) * 2.0;
c[k].imag = (b1.imag * v1.real) / (double)(N) * 2.0;

Case cos(2Pi*k/N) >= 0

For cos(2Pi*k/N) >= 0 Reinsch takes the sum instead of the difference:

v[n] + v[n-1] = y[n] - a1 * v[n-1] - v[n-2] + v[n-1]

and gets

(2cos(2Pi*k/N) + 2) = 4 * cos(Pi*k/N)^2

and

v[n] = dv[n] - v[n-1]

and that’s like:

a1.real = 4 * Math.Pow(Math.Cos((double)(Math.PI * (double)(k) / (double)(N))), 2.0);
a1.imag = 0;
we[k].real = a1.real;
for (n = 0; n < N; n++)
{
      dW = y[n].real + a1.real * v1.real - dW;
      v0.real = dW - v1.real;
      v1 = v0;
}
c[k].real = (dW - a1.real / 2.0 * v0.real) / (double)(N) * 2.0;
c[k].imag = (b1.imag * v1.real) / (double)(N) * 2.0;

The instability of the Görtzel algorithm was caused by extinction of numbers after floating point in earlier time. That could have happened if the whole algorithm was implemented with float variables which had a precision of 7 digits after floating point. Implemented like this with more than 28000 samples cos(2Pi*k/N) got 1.0 with k = 1. But nowadays with double values, this does not happen anymore. So the two algorithms behave the same still with 100000 samples. That means there is no need for a Reinsch algorithm as long as the DFT is performed on a modern 64 Bit computer and is implemented in a modern language like C#

For the analytic Fourier transformation of the used sample signals see Fourier transformation

C# Demo Project DFT Reinsch algorythm

DFT_Reinsch.zip

Java Demo Project DFT Reinsch algorythm

DFT_Reinsch.zip