The Newton-Gregory interpolation algorithm is a modified version of the Newton interpolation algorithm (see Newton interpolation) it is basically defined for equally spaced supporting points and a distance between them of 1. It uses the similar polynomial for the interpolation of yp
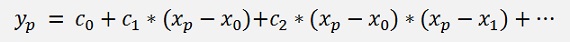
But the coefficients c0 to cn are a bit different and there are 2 versions of Newton-Gregory algorithm: The forward and the backward interpolation.
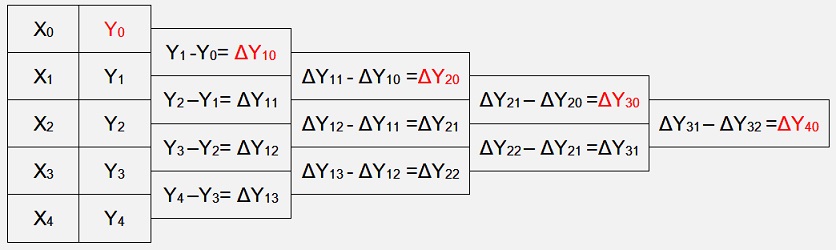
The Newton-Gregory algorithm uses a bit a simpler approach to calculate the ci factors. It builds differences of yi in multiple layers.
With 5 supporting points that would look like:
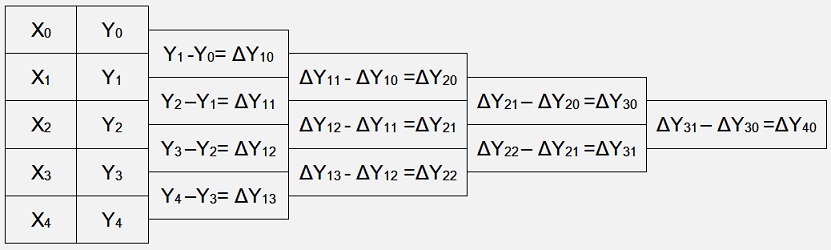
There are 2 approaches to interpolate a point between 2 supporting points. The literature says a point close to x0 is interpolated by a forward interpolation and a point close to xn should be interpolated by a backward interpolation. I say it does not depend that much
The
algorithm anyhow works only for not too many supporting points and
there both, forward and backward interpolation work more or less the
same.The Newton-Gregory forward interpolation uses
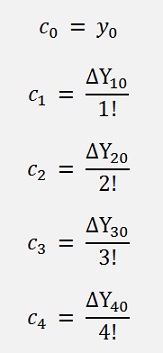
And so on.
To visualize in the above table there are only the red values used:
If the ΔY values are calculated from the yi values that is:
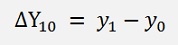
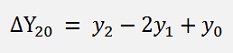
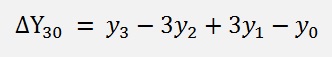
Binominal series
So ΔY40 could be written as
Whereas
That’s an easy way to calculate all the ΔY values.
If we replace c0 to cn by the formulation for ΔY now, that looks like this:
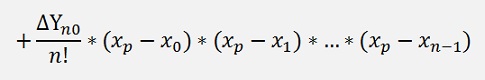
and if we separate the parts
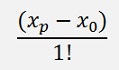
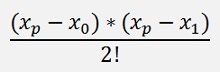
to
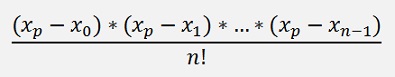
and keep in mind that ΔX = 1 and set X0 = 0.
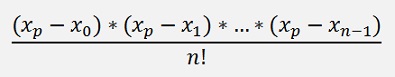
Can be written as:
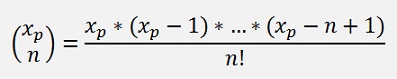
A binominal factor. Even if is Xp is no integer.
With this the interpolated value becomes:
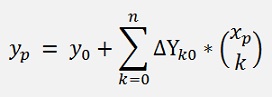
And if ΔY00 = Y0
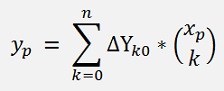
That gives a light algorithm where the same function to calculate the binominal factor
public double Binom(double n, double k)
{
{
double i, j;
double res = 1.0;
j = 0;
if ((k != 0) && (k != n))
{
return res;
}double res = 1.0;
j = 0;
if ((k != 0) && (k != n))
{
for (i = 0; i < k; i++)
{
for (i = 2.0; i <= k; i++)
{
}{
res = res * (n - j);
j++;
}j++;
for (i = 2.0; i <= k; i++)
{
res = res / i;
}return res;
can be used to calculate the ΔY values and the interpolated value.
The function that computes the ΔY elements looks like:
void CalcElements(double[] y)
{
int i, j;
double sign = 1;
for (i = 0; i < y.Length; i++)
{
}double sign = 1;
for (i = 0; i < y.Length; i++)
{
c[i] = 0;
sign = 1;
for (j = 0; j < i + 1; j++)
{
if (i % 2 != 0)
c[i] = -c[i];
}sign = 1;
for (j = 0; j < i + 1; j++)
{
c[i] = c[i] + sign * y[y.Length - j - 1] *
Binom(i, j);
sign = -sign;
}sign = -sign;
if (i % 2 != 0)
c[i] = -c[i];
This function computes the ΔY elements and puts them into the double array c.
And the interpolation for one point is done in
double Interpolate(double xp, int order)
{
int i, k;
double tempYp = 0;
for (i = 0; i < order; i++)
{
return tempYp;
}double tempYp = 0;
for (i = 0; i < order; i++)
{
tempYp = tempYp + Binom(xp / deltaX, i) * c[i];
}return tempYp;
An important detail to remark is that Xp runs from 0 to Xn. It is in reality Xp – X0.
A second detail is the fact that our ΔX = 1 so far. That means if in reality ΔX <> 1, it has to be corrected. That’s why xp is divided by deltaX in the Interpolation function.
The complete sequence to compute the interpolated curve is:
CalcElements(y_k, order);
for (i = 0; i < datapoints; i++)
{
xp[i] = (double)(i) * x_k[order - 1] / (double)(datapoints);
yp[i] = Interpolate(xp[i], order);
}yp[i] = Interpolate(xp[i], order);
This function uses datapoints as the number of data points to compute and puts the points into the array xp and yp. From there the curve can be drawn.
The Newton-Gregory backward interpolation does the same as the forward one. It only runs backward. So it uses
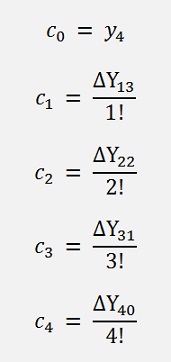
In the table from further above the red values:
Then the interpolation runs backward to. Instead of 0 to Xn – X0 it runs from Xn – X0 to 0.
That makes the function to compute the c values a bit different:
void CalcElements(double[] y)
{
int i, j;
double sign = 1;
for (i = 0; i < y.Length; i++)
{
c[i] = 0;
sign = 1;
for (j = 0; j < i + 1; j++)
{
c[i] = c[i] + sign * y[j] * Binom(i, j);
sign = -sign;
}
(i % 2 != 0)
c[i] = -c[i];
}
}
In the 11. row y runs in the opposite direction
The sequence to compute all data points becomes a bit different to.
CalcElements(y_k, order);
for (i = datapoints-1; i >= 0; i--)
{
xp[i] = x_k[order - 1] - (double)(i) * x_k[order - 1] / (double)(datapoints);
yp[i] = Interpolate(xp[i], order);
xp[i] = (double)(i) * x_k[order - 1] / (double)(datapoints);
}
Here xp is initialized backward first just to compute the yp values and afterwards it is reinitialized forward in order to be used for the output.
The Newton-Gregory algorithm interpolates the sample data
similar to a Polynomial interpolation, Lagrange or Newton interpolation algorithm. The curve looks like:
A bit overshooting (because the supporting points jump up and down quite much). But besides that it’s quite o.k.
With more supporting points things can change (similar to the other interpolation algorithms) Using y = 1 / x as function both the forward and the backward interpolation start to get mad at around 35 supporting points: The forward interpolation gets inaccurate at the right end of the graph
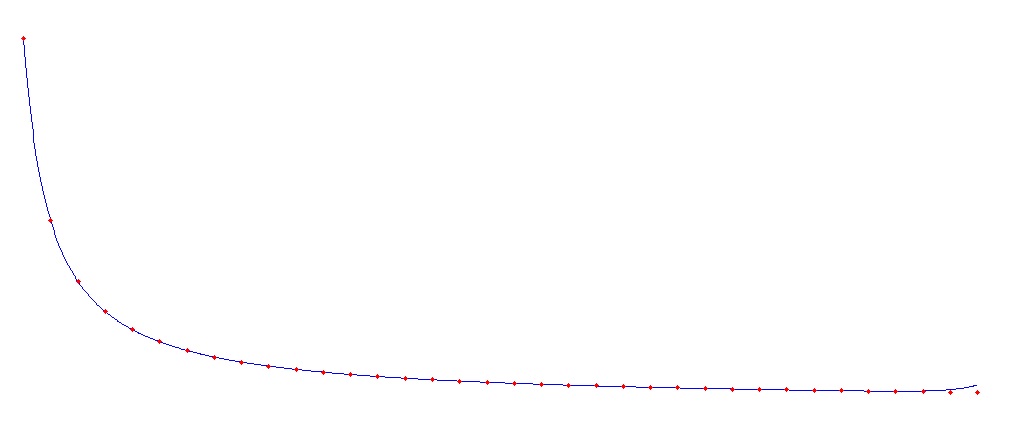
And the backward interpolation at the left side
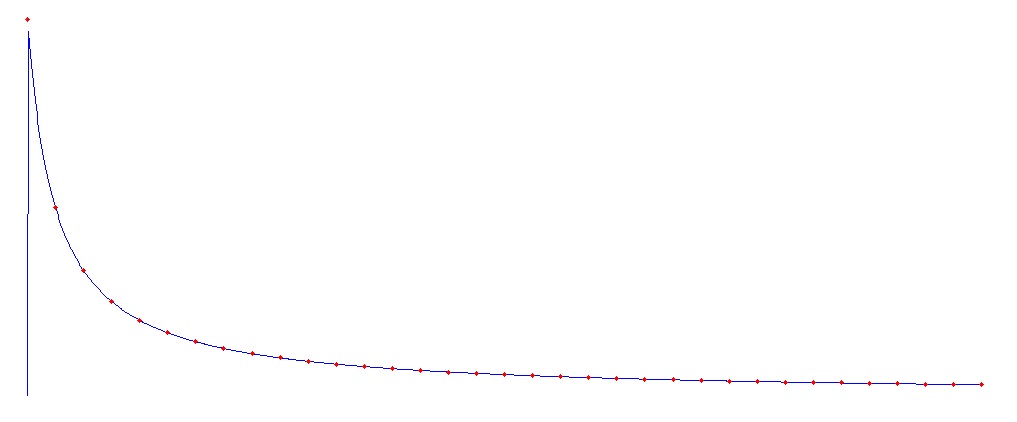
That’s what is mentioned in most literature about this algorithm
The Newton-Gregory interpolation algorithm is quite a lean algorithm to interpolate data points as long as there are not too many of them.
To deal with more supporting points I prefer the algorithm introduced by Newton himself (see Newton interpolation) . It’s a bit more complicate but it can handle up to 50 supporting points.