The 4th degree polynomial is the highest degree polynomial of which the root can be calculated analytically and it’s quite a demanding task to be done
 .
.But even more so it’s a cool algorithm.
The polynomial must have the form
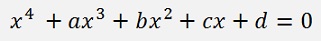
The approach is now to divide this polynomial by the 2th degree polynomial (x2 + px + q). This division yields another 2th degree polynomial and some leftover like
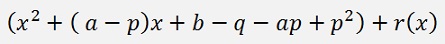
or with
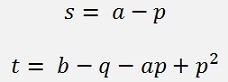
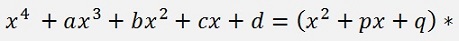
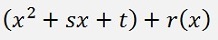
and the leftover r(x) is
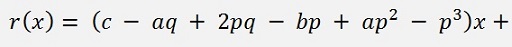
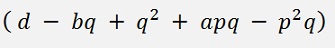
Now the idea is: If this leftover becomes 0, there are only the 2th degree polynomials
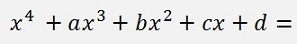
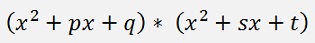
and the solution is the root of these 2 polynomials. Which is an easy task to be found.
To get
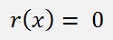
means
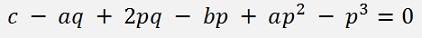
and
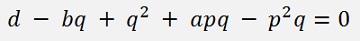
Both must be 0.
To solve that. From the upper equation
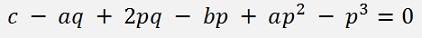
We get:
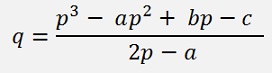
The lower equation
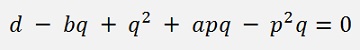
a bit reformed
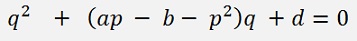
And the equation for q from above inserted:
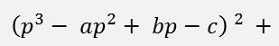
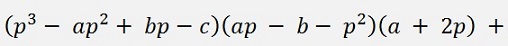
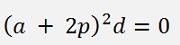
(The denominator can be neglected)
To simplify this formula is a hell of a calculation

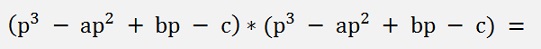
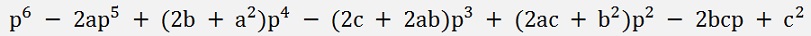
and
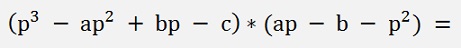
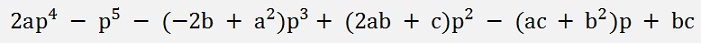
and this multiplied by (2p – a)
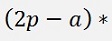
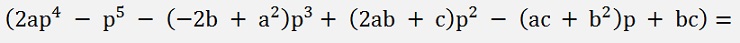
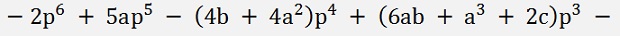
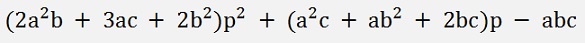
And all put together the resulting equation:
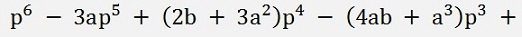
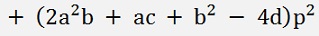
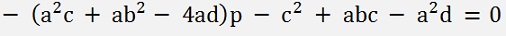
Now we have a 6th degree polynomial. Even worse than the origin polynomial

But it can be reduced to a 3th degree polynomial by a little substitution:
If we substitute
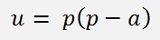
and
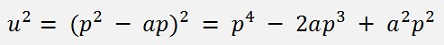
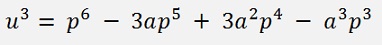
The 6th degree polynomial becomes:
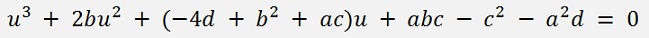
And that can be solved by the algorithm of Cerolamo Cardano.
But we are not at the end with this. Now we have u and first have to go back to p.
As we substituted
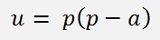
We have the quadratic equation
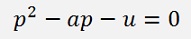
What corresponds to the equation in the article about the Quadratic equation
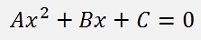
and has the solution:
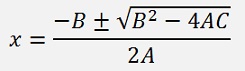
A parameter comparison shows:
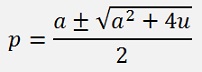
And with this p we can calculate q with the formulation from further above:
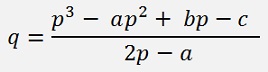
And the parameters of the first polynomial of
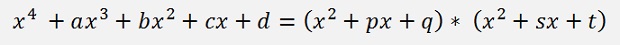
Are found
The second polynomial is given by
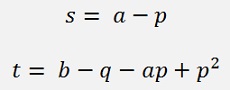
Are found
And with this the roots of both polynomials can be calculated by:
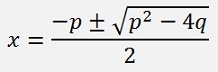
For the first
and
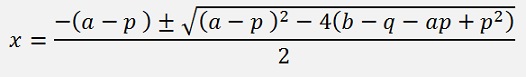
for the second one.
All 4 solutions can be complex if the part inside the square root is negative.
But there remains a special case. As there is a division in the expression
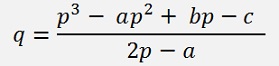
There is the question: What happens if 2p - a = 0? That makes things even a little bit easier.
There are still two expressions that should become 0:
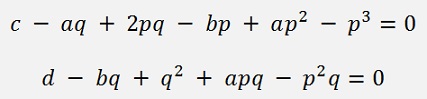
But if a = 2p, the upper expression becomes:
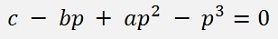
And as a = 2p we replace p = a/2
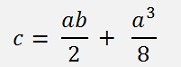
This is the indication that there is the special case a = 2p.
In the second expression
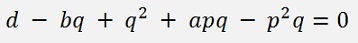
we do the same replacement p = a/2
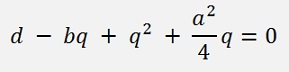
Or a bit nicer arranged:
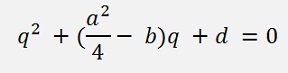
If the part inside the brackets is multiplied by a/a we get
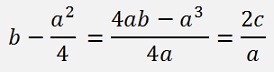
and so
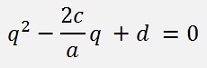
This quadratic equation can be solved with:
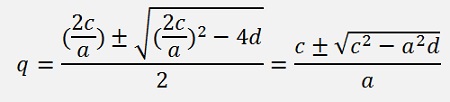
And p is already defined in this special case:
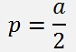
Now inside this special case there is another special case: What happens if a = 0?
With the condition
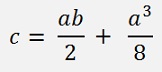
It’s clear that if a = 0 then c = 0 as well. That means the origin 4th degree polynomial becomes:
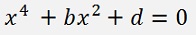
A quadratic equation of x2 and its solution is
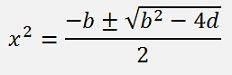
There are 2 solutions for x2 and the searched roots are the square roots of them. If b2 – 4d is negative, x2 will be complex and the square root of x2 has 2 solutions. What means that there are again 2 solutions for each square root and booth can be real or complex too.
To calculate the square root of a complex number we first have to transform the complex number into its polar form with its length
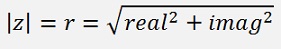
and it has an angle φ given by real and imag part:
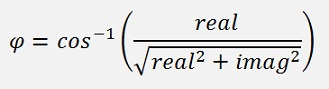
and if imag < 0
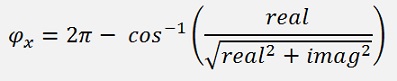
The square root of x2 is now the square root of the length:
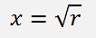
And the angle
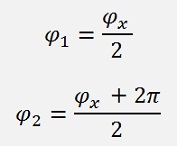
There are 2 solutions (see Complex numbers)
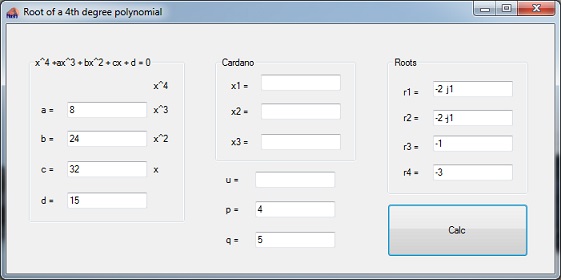
The demo project consists of one main window that shows all computed parameters if they are available.