The title integration by the use of Legendre polynomials is a bit misguiding as the effective integration is not done by Legendre polynomials. It is based on the Newton-Cotes formulation that uses the interpolation by Joseph-Louis Lagrange (See Lagrange interpolation for an introducition to the Lagrange interpolation) .
The Legendre polynomials are only used to figure out the supporting points for the Lagrange interpolation polynomials. The description of the integration by the Newton-Cotes formulation can be found on Integration by the Newton-Cotes formula
The idea behind the use of the Legendre polynomials is to distribute the supporting points in a way the Lagrange interpolation creates the least inaccuracy and therefore the integration done of these supporting points becomes the most accurate. This can be achieved by placing the supporting points at the roots of a Legendre polynomial or Chebychev polynomial.
The formulation of a Legendre polynomial Pn(x) is:
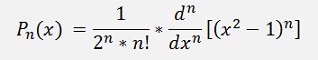
and it is defined for n = 0, 1, 2, …. And -1<= x <=1.
This formulation extended gives
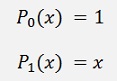
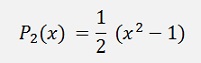
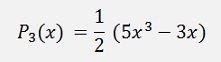
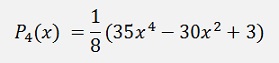
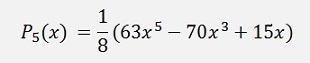
and so on…
This can be written in a recursive formulation as:
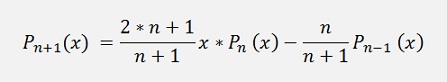
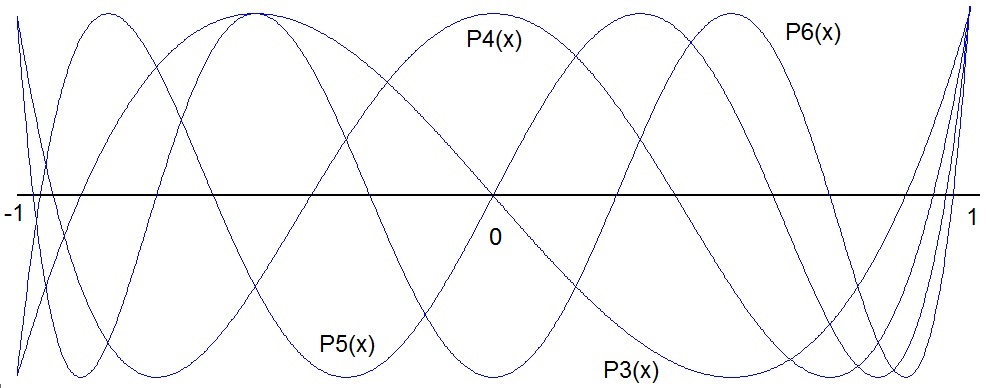
The graphs of these Legendre polynomials look like
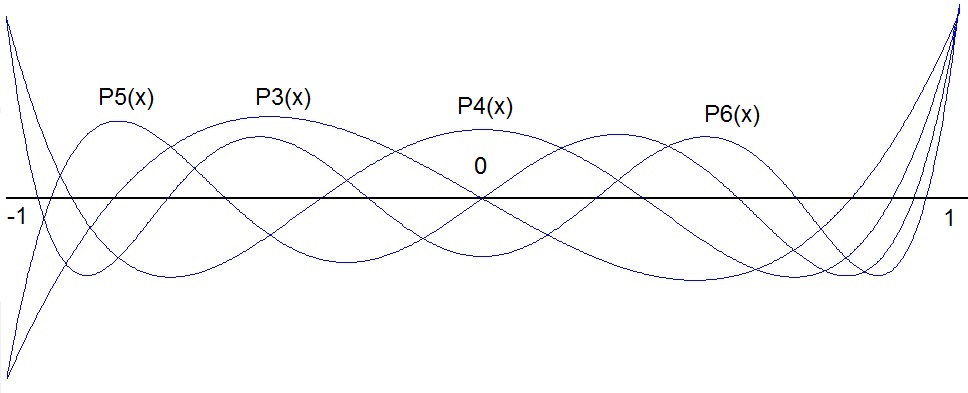
And they have roots symmetrical to 0.
The wave form of these graphs shows that the roots are symmetric to 0 and rather concentrated at both limits -1 and +1. That means if we place the supporting points there where these roots are, the distance between the points close -1 and +1 will be smaller than the distance of the supporting points close to 0. Now the distance between the supporting points closer to the limits has a bigger impact onto the inaccuracy than the distance of the supporting points close to the middle of the range of the function. In fact the inaccuracy for the Lagrange interpolation of n supporting points is the smallest if the supporting points are placed at the roots of the Legendre polynomial of the order n.
The only problem is to find these roots. With rising order of the polynomial an analytical solution becomes quite complicate quite quick. But the Legendre polynomials don’t have complex roots and they can be found by a Newton-Maehly algorithm (See Roots of a polynomial for an introducition to the Newton Maehly algorithm) .
The only task that is needed is to build the Legendre polynomial and this can be done out of the formulation
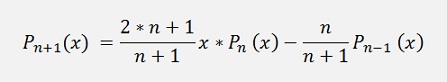
With
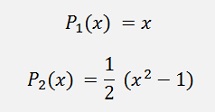
The C# function for this looks like:
public double[] CalcLegendre(int n)
{
double[]
p2 = new double[3]; // P2 =
1/2*(3x^2 - 1)
double[] p1 = new double[2]; // P1 = x
double[] poly = new double[n];
int i;
p2[2] = -0.5;
p2[1] = 0;
p2[0] = 1.5;
p1[1] = 0;
p1[0] = 1.0;
for (i = 2; i < n; i++) // loop from p2 to pn
{
return poly;
}double[] p1 = new double[2]; // P1 = x
double[] poly = new double[n];
int i;
p2[2] = -0.5;
p2[1] = 0;
p2[0] = 1.5;
p1[1] = 0;
p1[0] = 1.0;
for (i = 2; i < n; i++) // loop from p2 to pn
{
poly
=
NextLegendre(p2, p1, i);
p1 = p2;
p2 = poly;
}p1 = p2;
p2 = poly;
return poly;
with
private double[] NextLegendre(double[] pn2, double[] pn1, int n)
{
int
i;
double[] tempPoly = new double[pn2.Length + 1];
for (i = 0; i < pn2.Length; i++)
{
for (i = 0; i < pn1.Length; i++)
{
return tempPoly;
}double[] tempPoly = new double[pn2.Length + 1];
for (i = 0; i < pn2.Length; i++)
{
tempPoly[i]
= pn2[i] * (2 * n + 1) / (n + 1);
}for (i = 0; i < pn1.Length; i++)
{
tempPoly[i
+ 2] = tempPoly[i + 2] - pn1[i] * n / (n + 1);
}return tempPoly;
The function CalcLegendre returns a Legendre polynomial of the order n with the highest power of x in the first element.
The roots of this Legendre polynomial I compute by the Newton-Maehly algorithm in the function FindRoots() which puts the roots into the array of x.
Now there comes a step that is most often named calculating the weighting factors of the supporting points in the literature. I regard this as a bit unhappy as it is a computation of the Lagrange polynomials and building the integral of each. So I would rather call this step calculating the integration factors.
For the computation of the Lagrange polynomials and building the integral I used the same function I already implemented for the Newton-Cotes algorithm (see Integration by the Newton-Cotes formula ):
private double CalcWeights(int index)
{
int
i;
double a = -1;
double b = 1;
double res = 0;
double[] wl = new double[1];
double[] poly = new double[2];
wl[0] = 1;
// build polynomial
for (i = 0; i < x.Length; i++)
{
// build integral
res = wl[0] * (b - a);
for (i = 1; i < x.Length; i++)
{
return res;
}double a = -1;
double b = 1;
double res = 0;
double[] wl = new double[1];
double[] poly = new double[2];
wl[0] = 1;
// build polynomial
for (i = 0; i < x.Length; i++)
{
if
(i != index)
{
}{
poly[0]
=
-x[i] / (x[index] - x[i]);
poly[1] = 1 / (x[index] - x[i]);
wl = multPoly(wl, poly);
}poly[1] = 1 / (x[index] - x[i]);
wl = multPoly(wl, poly);
// build integral
res = wl[0] * (b - a);
for (i = 1; i < x.Length; i++)
{
res
= res
+ wl[i] * (Math.Pow(b,
i + 1) - Math.Pow(a,
i + 1)) / (i + 1);
}return res;
This function returns one weighting factor for the supporting point at index and with this the integration can be put together. There is only one thing that remains. Due to the fact, that the Legendre polynomials are defined from -1 to 1 and therefore the roots are in this range to and the weighting factors are related to this range as well, we have to transform them to the actual range of the integration.
If the integration should run from a to b, first the supporting points are built like:
for (i = 0; i < order; i++)
{
y_k[i]
= f_x(a + (b - a) * (1 - x[i]) / 2);
}With f_x(..) carrying the function that should be integrated.
After that the integral can be computed in a loop and finally transformed to the range a to b as:
integral = 0;
for (i = 0; i < order; i++)
{
integral = integral + y_k[i] * CalcWeights(i);
}
integral = integral / 2 * (b - a);
That’s it

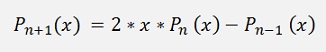
Not too much different from the graphs of the Legendre polynomials.
For the computation of the Chebychev polynomials I implemented the function
public
double[]
CalcLChebychef(int
n)
{
{
double[]
p2 = new double[3]; // P2 = 2x^2 - 1
double[] p1 = new double[2]; // P1 = x + 0
double[] poly = new double[n];
int i;
p2[2] = -1;
p2[1] = 0;
p2[0] = 2;
p1[1] = 0;
p1[0] = 1;
for (i = 2; i < n; i++) // loop from p2 to pn
{
return poly;
}double[] p1 = new double[2]; // P1 = x + 0
double[] poly = new double[n];
int i;
p2[2] = -1;
p2[1] = 0;
p2[0] = 2;
p1[1] = 0;
p1[0] = 1;
for (i = 2; i < n; i++) // loop from p2 to pn
{
poly
=
NextChebychev(p2, p1, i);
p1 = p2;
p2 = poly;
}p1 = p2;
p2 = poly;
return poly;
private
double[]
NextChebychev(double[]
pn2, double[]
pn1, int
n)
{
{
int
i;
double[] tempPoly = new double[pn2.Length + 1];
for (i = 0; i < pn2.Length; i++)
{
for (i = 0; i < pn1.Length; i++)
{
return tempPoly;
}double[] tempPoly = new double[pn2.Length + 1];
for (i = 0; i < pn2.Length; i++)
{
tempPoly[i]
= pn2[i] * 2;
}for (i = 0; i < pn1.Length; i++)
{
tempPoly[i
+ 2] = tempPoly[i + 2] - pn1[i];
}return tempPoly;
To compute the complete integral I use the sequence
l =
CalcLegendre(order);
FindRoots();
Integrate();
FindRoots();
Integrate();
l =
CalcLChebychef(order);
FindRoots();
Integrate();
FindRoots();
Integrate();
Finally I made a small comparison of the integration using the Newton-Cotes formulation with equal distances between the supporting points and using the Legendre or Chebychev polynomials to place them. Therefor I used the function
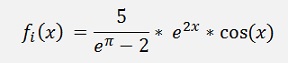
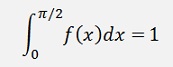
The results of these calculations are:
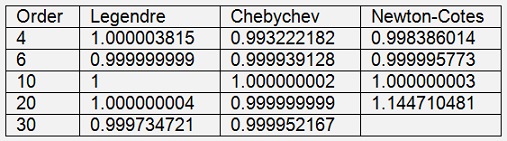
The inaccuracy of these samples is
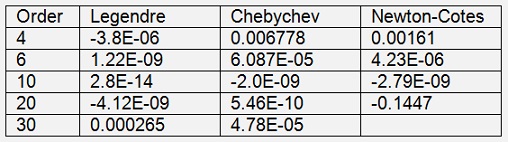
It’s interesting to see that the algorithm using constant distances (Newton-Cotes) is quite close to the Legendre and the Chebychev algorithm if there are 10 supporting points used. But with more supporting points it becomes very inaccurate soon.
Using Legendre polynomials seems to be a good idea if the number of supporting points is small. But with more than 20 supporting points the Chebychev algorithm seems to be the better solution. But still it gets to its limits with 30 supporting points and becomes more and more inaccurate with higher numbers of supporting points. But never the less: All 3 algorithms are quite cool


