To solve a matrix equation by Gram-Schmidt QR decomposition
Basically

I first got into touch with the Gram-Schmidt (Jørgen Pedersen Gram and Erhard Schmidt) algorithm in relation with some Eigenvalue computations. Unfortunately the Gram-Schmidt algorithm is rather instable in iteration and therefore not too useful for Eigenvalue computations. So I had to leave that. But there is still an interesting application.

There are 2 algorithms of Gram-Schmidt mentioned in the literature: The Gram-Schmidt orthogonalization and the orthonormalization. In this article I’m writing about the orthonormalization which can be extended to a QR decomposition. This QR decomposition can be used to implement quite a lean algorithm to solve a matrix equation.
The Gram-Schmidt orthonormalization builds from a matrix M a matrix Q which is orthonormal and with Q and M a right upper matrix R is calculated according to:

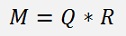
GramSchmidt


In the case of a matrix equation the following point is interesting:

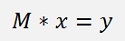
GramSchmidt


If M is substituted by Q * R, the matrix equation gets the form

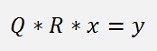
GramSchmidt

And now both sides can be multiplied by QT (see Transposed Matrix) and that eliminates Q on the left side:

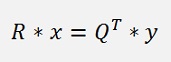
GramSchmidt


With this we get a right upper diagonal matrix on the left side remaining which means no further elimination is required and the matrix equation can be solved right away. On the right side the solution vector y is multiplied by the transposed matrix of Q. That yields another vector and is no complicate operation :-)



Gram-Schmidt orthonormalization

The Gram-Schmidt orthonormalization calculates column by column from M the orthonormal matrix Q. For each column first an orthogonal vector is built (not the same as is done in the Gram-Schmidt orthogonalization) and then normalized by dividing it by its length. The first column is the easiest. If m1 is the first column vector of M and q1 is the first column vector of Q:

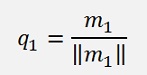
GramSchmidt

For all other columns the formulation is a bit different and requires some more steps and an arbitrary vector vk:

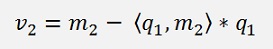
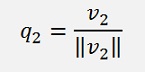
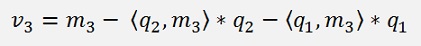
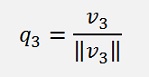
GramSchmidt

GramSchmidt

GramSchmidt

GramSchmidt

And so on:


For k > 1 that’s:

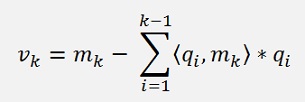
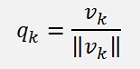
GramSchmidt

GramSchmidt



Whereas

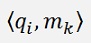
GramSchmidt



is the so called inner product of the two vectors qi and mk. Which is basically the same as the dot product of qi and mk in this case.

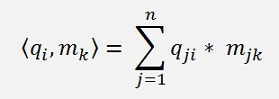
GramSchmidt



That’s for Q.


Now R has to be computed with that.


With

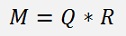
GramSchmidt



To eliminate Q on the right side, the equation is extended by QT again and that gives

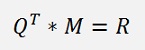
GramSchmidt



For a 4*4 matrix that would be:

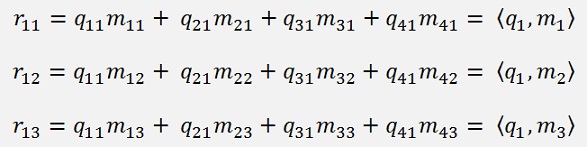
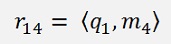
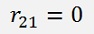
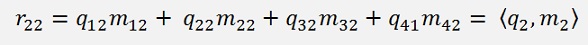
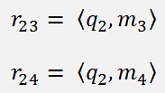
GramSchmidt
GramSchmidt
GramSchmidt
GramSchmidt
GramSchmidt



And so on. All the elements below the main diagonal become 0. That comes from the way qk is built. If the index k of qk is bigger than the index j of mj the dot product of them becomes 0.

For the entire matrix R:

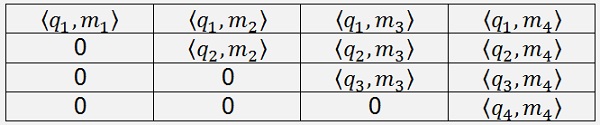
GramSchmidt



Most these values are already computed in the part for Q. only the first element must be computed in advance and all die diagonal elements must be computed afterwards.



In C# the entire calculation would be a function like:


public void CalcGranSchmidt(int order)
{
int i, k;
int actCol;
double len = 0.0;
double[] v = new double[order];
for (i = 0; i < order; i++)
{
len = len + m[i, 0] * m[i, 0];
}
len = Math.Sqrt(len);
 
// q1 is different
for (i = 0; i < order; i++)
{
q[i, 0] = m[i, 0] / len;
}
 
//r11 can be calculated right away
r[0, 0] = InnerProd(m, m, 0, 0, order)/len;
 
for (actCol = 1; actCol < order; actCol++)
{
for (i = 0; i < order; i++)
{
v[i] = m[i, actCol];
q[i, actCol] = 0.0;
}
 
for (i = 0; i < actCol; i++)
{
// calculate the elements of R
r[i, actCol] = InnerProd(q, m, i, actCol, order);
 
// calculate the temporary V vector
for (k = 0; k < order; k++)
{
v[k] = v[k] - q[k, i] * r[i, actCol];
}
}
 
// the length of V
len = Len(v);
 
// one column od Q is V / lenght of V
for (i = 0; i < order; i++)
{
q[i, actCol] = v[i] / len;
}
 
// the diagonal elements of R must be calculated separately
r[actCol, actCol] = InnerProd(q, m, actCol, actCol, order);
}
}




with


double InnerProd(double[,] a, double[,] b, int colA, int colB, int order)
{
int i;
double c = 0;
for (i = 0; i < order; i++)
{
c = c + a[i, colA] * b[i, colB];
}
return c;
}



for the inner product of two column vectors and


double Len(double[] a)
{
int i;
double len = 0.0;
for (i = 0; i < a.Length; i++)
{
len = len + a[i] * a[i];
}
len = Math.Sqrt(len);
return len;
}



for the length of a vector.


After that the resulting matrixes Q and R computed from


double[,] m = new double[MaxOrder, MaxOrder];


are in the arrays


double[,] q = new double[MaxOrder, MaxOrder];
double[,] r = new double[MaxOrder, MaxOrder];


From here we can go back to our main goal: To solve a matrix equation.

From the basic equation

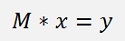
GramSchmidt

We came to

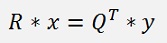
GramSchmidt

R and Q we have got now. In a next step QT * y must be computed. The vector y is the solution vector of the matrix equation:
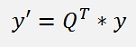
GramSchmidt


is done with the function

public double[] MultMatrixTransVect(double[,] tr, double[] b)
{
int j, k;
double[] al = new double[b.Length];
double[] yl = new double[b.Length];
 
for (j = 0; j < b.Length; j++)
{
al[j] = 0.0;
for (k = 0; k < b.Length; k++)
{
al[j] = al[j] + (tr[k, j] * b[k]);
}
}
return al;
}



called like:

y = MultMatrixTransVect(q, y);



And then the matrix equation looks like:

GramSchmidt


And this can be solved right away

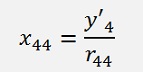
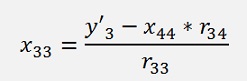
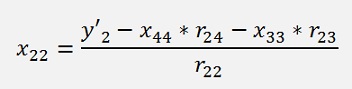
GramSchmidt
GramSchmidt
GramSchmidt


And so on.


In a function that’s


public void Solve()
{
int k, l;
for (k = MaxOrder - 1; k >= 0; k--)
{
for (l = MaxOrder - 1; l >= k; l--)
{
y[k] = y[k] - x[l] * r[k, l];
}
x[k] = y[k] / r[k, k];
}
}




And the solution of the matrix equation is placed in


double[] x = new double[MaxOrder];



The Gram-Schmidt orthonormalization is not a real orthonormalization. The columns do not always become fully orthonormal to each other. But still it’s quite a cool algorithm :-)

C# Demo Project to solve a matrix equation by Gram-Schmidt QR decomposition

  • Matrix_Gram_Schmidt.zip


    • Java Demo Project to solve a matrix equation by Gram-Schmidt QR decomposition

  • MatrixGamSchmidt.zip