Cholesky decomposition

The Cholesky decomposition is an approach to solve a matrix equation where the main matrix A is of a special type. It must be symmetrical to the main diagonal, element a₁₁ must be positive and the other elements in the main diagonal must be bigger than or at least as big as the square of the other elements in the same row. Mathematically it is said the matrix must be positive definite and Hermitian. But does anybody understand this? :-)

Cholesky’s idea is to decompose the matrix A of the matrix equation Ax= b into a lower triangle matrix L and its transposed matrix L^T and substitute A to LL^Tx = b. With these 2 matrixes the equation can be solved in 2 quite simple loops. Therefore another vector y is introduced and the equation LL^Tx = b is separated into

Ly = b

and

L^Tx = y

First the parameters of y can be calculated and with these we get the parameters of x which is the solution of the matrix equation. But let’s start at the beginning.

LL^T separation

First the matrix A has to be decomposed into this L- and L^T-matrix:

For this we have to start by the multiplication of the 2 matrixes L and L^T (therefore I use a 4*4 matrix. The result will be valid for n*n matrixes as well)

L * L^T =

and confront it with the originating matrix A

Parameter comparison of the parameters in the first row shows:

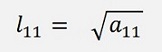
(That shows why all the element a11 must be bigger than 0)

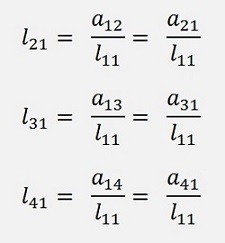
That’s the first column of L

From

a₂₂ = l₂₁ * l₂₁ + l₂₂ * l₂₂

we get

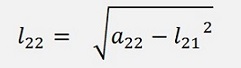
There are some more roots like this. That’s why the diagonal elements should be bigger than or equal to the squares of the other elements in the same row.

a₃₂ = l₂₁ * l₃₁ + l₂₂ * l₃₂

gives

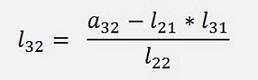
and

a₄₂ = l₄₁ * l₂₁ + l₄₂ * l₂₂

gives

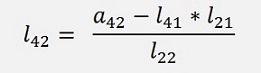
and we got the elements of the second row.

And the third row is

a₃₃ = l₃₁ * l₃₁ + l₃₂ * l₃₂ + l₃₃ * l₃₃

from this

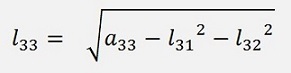
a₄₃ = l₄₁ * l₃₁ + l₄₂ * l₃₂ + l₄₃ * l₃₃

and so

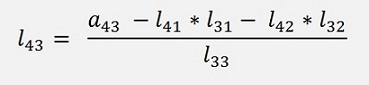
and finally

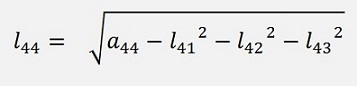
But how can this be put into an algorithm?

If we look at the elements below the main diagonal, we can see: They are all built by a fraction that consists of a_ij minus some l elements.

That can be written as

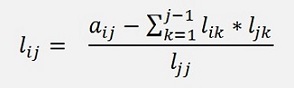
For i > j

And for the main diagonal

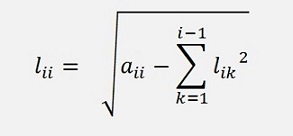
This can be put into code like:

private void Cholesky_decomp()
{
     int i, j, k;
     for (i = 0; i < MaxOrder; i++)
     {
          for (j = 0; j <= i; j++)
          {
              if (i > j)
              {
                   l[i, j] = a[i, j];
                   for (k = 0; k < j; k++)
                        l[i, j] = l[i, j] - l[i, k] * l[j, k];
                   l[i, j] = l[i, j] / l[j, j];
              }
              if (i == j)
              {
                   l[i, i] = a[i, i];
                   for (k = 0; k < j; k++)
                   {
                        l[i, i] = l[i, i] - (l[i, k] * l[i, k]);
                   }
                   l[i, i] = Math.Sqrt(l[i, i]);
              }
          }
     }
}

(The return value will be false if there was a calculation error)

This function calculates the matrix L. L^T can be got from this by switching the indexes.

Unfortunately we are not done jet. There is still some math to be survived 

Solving the equation

We want to solve a matrix equation and therefore we have to resolve Ly = b

Carrying out this multiplication and resolving for y gives:

The same we have to do for L^Tx = y now

Here the multiplication and resolving for x gives:

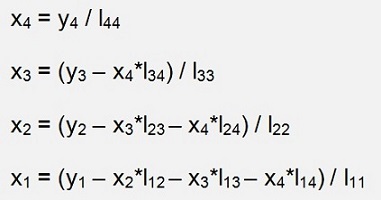
and the vector x is the solution of our matrix equation.

These 2 sequences can be implemented in 2 loops like:

private void Solve()
{
     int i, j;
     for (j = 0; j < MaxOrder; j++)
     {
         y[j] = d[j];
         for (i = 0; i < j; i++)
         {
              y[j] = y[j] - y[i] * l[j, i];
         }
         y[j] = y[j] / l[j, j];
     }
     x[MaxOrder - 1] = y[MaxOrder - 1] / l[MaxOrder - 1, MaxOrder - 1];
     for (j = MaxOrder - 2; j >= 0; j--)
     {
         x[j] = y[j];
         for (i = MaxOrder - 1; i > j; i--)
         {
              x[j] = x[j] - x[i] * l[i, j];
         }
         x[j] = x[j] / l[j, j];
     }
}

Now we are almost done. There is only some exception handling missing. There are divisions by l_jj in Cholesky_decomp() and in Solve() and ujj can be 0 and before a root can be calculated, it has to be taken care that we don’t try to find the root of a negative value. This has to be handled. Therefore I extended Cholesky_decomp() to return its calculation success as a Boolean type and call Solve() only if this result is true.

Now the solution of our matrix equation is in the vector x.

With this a sample matrix equation of

I got the solution

The Cholesky decomposition is a quite smart approach to solve this special case of a matrix equation. Only this special case seems to be a bit constructed. But there are really cases where this type of matrix is realistic and it can be used. I use the Colesky decomposition in the method of the least squares and in the calculation of periodic splines. There it works perfect :-)

.

see

Method of the least squares

NaturalSplines

and for some related articles:

Singular value decomposition

Householder transformation

LU decomposition

Gram-Schmidt QR decomposition

C# Demo Project Cholesky decomposation

Matrix_Cholesky.zip