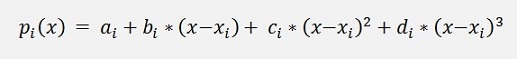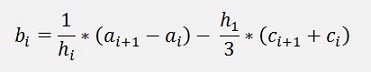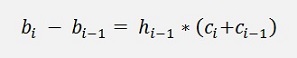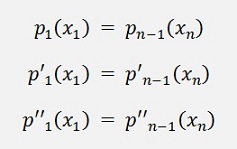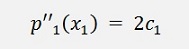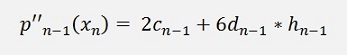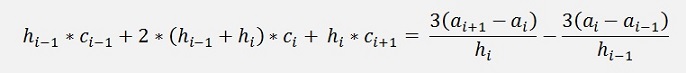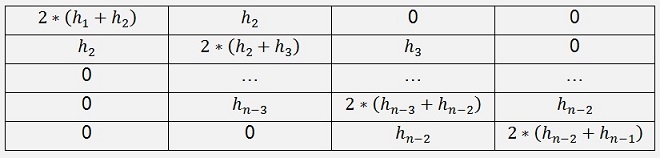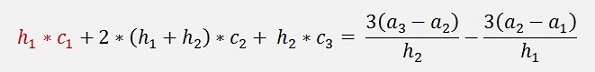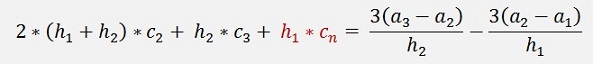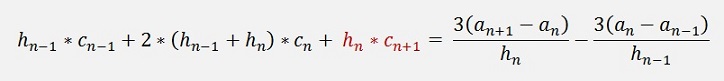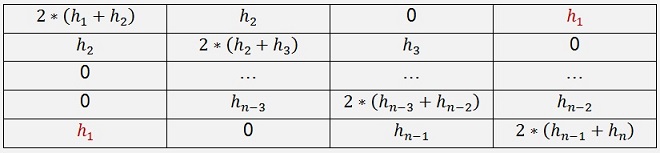Periodic splines

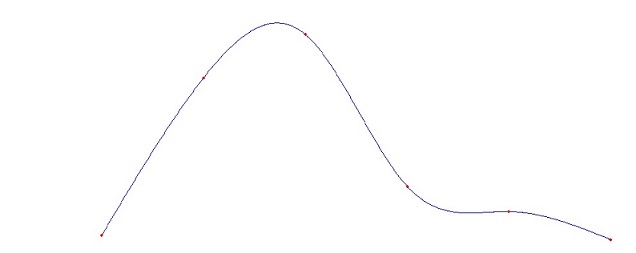
Periodic splines are meant to interpolate a function which is periodic to the interval between the first and the last supporting point. If we have for instance a set of 6 supporting points, the interpolation would look like this:


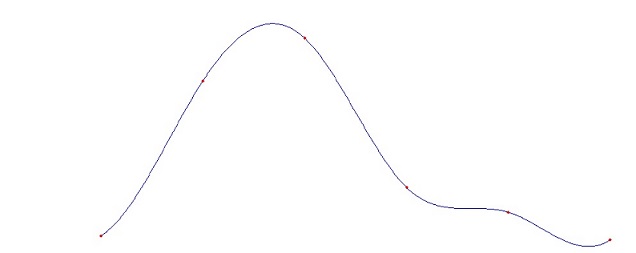
Whereas the spline function built by natural splines with the same supporting points would look like this


There is a small difference between these two graphs: On the periodic spline function the slope and function value at the end and the slope and function value at the beginning are equal. That means we could take the graph and copy and paste it at the end of the original graph without getting a jump or kink at the joint. On the natural splines that’s not possible. With periodic splines we interpolate a periodic function.

The mathematical base for periodic splines is the same as the one for natural splines . We have the same resulting function here too:




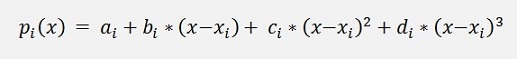
And there are the same conditions to be fulfilled:
a) The graph of the functions shall meet all the supporting points
 
pi (xi ) = yi for i = 1 to n-1
b) The graph shall not have a jump discontinuity at the supporting points
pi (xi ) = pi-1 (xi ) for i = 2 to n-1
 
c) There shouldn’t be any break-points at the supporting points
p'i (xi ) = p'i-1 (xi ) for i = 2 to n-1
 
d) The bending of the graph shall be the same on both sides of the supporting points
p''i (xi ) = p''i-1 (xi ) for i = 2 to n-1




Same as for the natural spline we get from condition b

And c yields:


But now there are some additional conditions to be fulfilled:

As the resulting function shall be one interval of a periodic function it should have the same slope and the same shape at the first and the last supporting point. That’s:



That means the conditions for the natural splines that were valid for I = 2 to n-1 are valid for I = 2 to n now and we have to extend the matrix equation to calculate the c parameters by one row and one column.

Another point is that



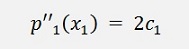
and



That shows c1 <> 0 for periodic splines and we have to calculate it. But c1 does not appear in the matrix equation.

The equation for the ci parameters is the same as we already got it for the natural splines



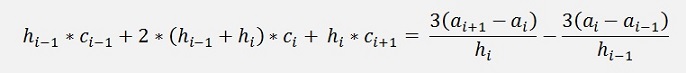
This equation led us to the following matrix equation for natural splines:



Whit the solution vector



This matrix equation we have to extend by one row and one column for the periodic splines. With this extension we get cn in the last column. But cn is not on the in the scope of the spline functions. That wouldn’t help us. The solution is the periodicity. As our spline function should interpolate a periodic function and a next period starts right on the right side of the last supporting point of our graph.



we can say cn is the same as c1. We calculate cn in the matrix equation and use it for c1 finally. If we have a look at the equation for the first line of the matrix equation:



c1 is already included. We just set it to 0 for natural splines. And as it was 0 anyway, we didn’t care that it didn’t appear in the matrix. Now it’s not 0 anymore but it still does not appear in the matrix. But we can write



And cn appears in the matrix.

Our matrix equation has the order n -1 now and runs from 2 to n now. The last row has the equation



Here we have the term cn+1 which is the same as c2 and we can write



Whit this and the fact that hn = h1 the matrix equation becomes like



the solution vector remains almost the same



For the solution vector is an = a1 and an+1 = a2. Now we can calculate all parameters. After solving the matrix equation we just have to set c1 = cn. An important point to consider is that we interpolate a period of a periodic function. That means the starting point and the end point must have the same y-value.
See Spline_periodic.zip

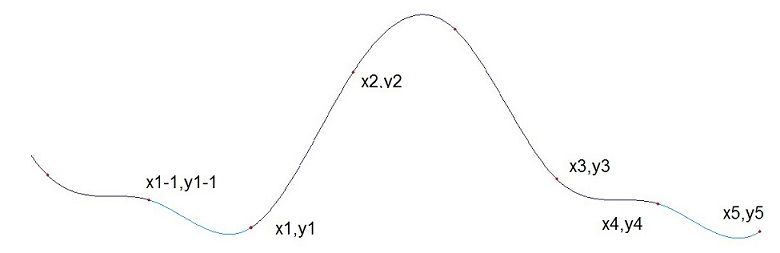
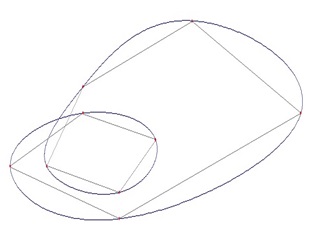
Closed loops
As a closed loop can be regarded as a periodic function, it can be interpolated by periodic splines.
That’s quite cool :-)



The only thing that has to be done is. We have to insert a kind of time stamp t to the x,y points and interpolate the x,t sequence and the y,t separate and put them together afterwards. To the sample sequence



I arbitrary add the time stamps



And calculate the spline parameters for x,t and y,t. With these I build a x,y shape as a function of t to get the above shape. This mechanism is used to draw contour lines on maps or field lines in electrical fields :-)



Using a Cholesky decomposition to solve the matrix equation

The Cholesky decomposition is a quite lean approach to solve a matrix equation with some boundary conditions. The main matrix must be symmetrical to its main diagonal and the elements of the main matrix must be positive and bigger than the square of the other elements in the same row. That’s the case here and so the Cholesky decomposition can be used to solve the matrix equation.
For a detailed description of the Colesky decomposition see (see Cholesky decomposation)


For Natural splines see natural splines

For End slope splines see end slope splines


C# Demo Project to periodic splines and xy function interpolating whit periodic splines

  • Spline_periodic.zip
  • Spline_XY.zip
  • Spline_XY_Cholesky.zip


    • Java Demo Project to periodic splines and xy function interpolating whit periodic splines

  • SplinePeriodic.zip
  • SplinePeriodicXY.zip